Esercizio 5 Problemi sul teorema di Talete e le sue applicazioni

-10

Traccia

La bisettrice di un angolo acuto di un triangolo rettangolo divide il cateto opposto in due segmenti lunghi 3 cm e 5 cm. Determinare il raggio della circonferenza circostritta al triangolo dato e la lunghezza della bisettrice. 5 e 3\sqrt 5

 

circonferenza circostritta a triangolo rettangolo

Svolgimento

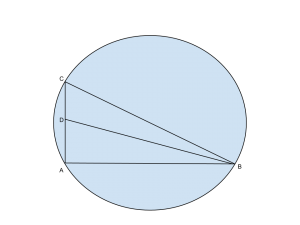
Sia ABC il triangolo rettangolo in A.

Dai dati avremo che:

AD=3 \mbox { cm}

DC=5 \mbox { cm}

Tracciando la bisettrice BD, e sfruttando il teorema della bisettrice notiamo che:

\frac {AB}{AD}=\frac {BC}{DC}

AB=\frac35 BC

Essendo un triangolo rettangolo, ponendo BC=x, sfruttiamo il teorema di Pitagora per ricavare l’incognita:

BC^2=AC^2+AB^2

x^2=64a^2+\frac {9}{25}a^2

\frac {16}{25}x^2=64a^2

\frac 45 x=8a

x=10a

Quindi:

BC= 10\mbox { cm}

AB=6 \mbox { cm}

Calcolare il raggio della circonferenza circoscritta è facile, in quanto, essendo ABC rettangolo, allora l ‘ipotenusa risulta essere il diametro e di conseguenza il raggio sarà la sua metà:

r=\frac 12 BC=5 \mbox { cm}

Calcoliamo ora la bisettrice:

BD =\sqrt{AB^2+AD^2}\mbox { cm} = \sqrt {36+9}\mbox { cm}=\sqrt {45}\mbox { cm}=3\sqrt 5\mbox { cm}

 

 

Altri esercizi simili:

 

(Questa pagina è stata visualizzata da 365 persone)

Lascia un commento