Samuele scrive: Equazione con valore assoluto

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Equazioni con valore assoluto

Corpo del messaggio:

1) \frac {\left|x^2-1 \right|}{x}=3-\left[\frac {2-\left|2x^2+x+3\right|}{x}\right]

 

 

Risposta dello staff

Notiamo subito che, nel secondo valore assoluto, il \Delta=1-24=-23 è negativo, e ciò implica che il polinomio è positivo per ogni valore dell’incognita. Quindi l’unico valore assoluto da studiare risulta essere:

x^2-1 \geq 0 \iff x \leq -1 \quad \lor \quad x \geq 1.

Quindi andiamo a risolvere i due sistemi:

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ \frac {x^2-1 }{x}=3-\left[\frac {2-2x^2-x-3}{x}\right]\end {cases} \quad \begin{cases} -1<x< 1 \\ \frac {1-x^2 }{x}=3-\left[\frac {2-2x^2-x-3}{x}\right]\end {cases}

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x \neq 0 \\ x^2-1 =3x-2+2x^2+x+3\end {cases} \quad \begin{cases} -1<x< 1 \\ x \neq 0 \\ 1-x^2 =3x-2+2x^2+x+3\end {cases}

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x \neq 0 \\ x^2+4x+2=0\end {cases} \quad \begin{cases} -1<x< 1 \\ x \neq 0 \\ 3x^2+4x=0\end {cases}

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x \neq 0 \\ x_{\frac 12}=\frac {-4\pm \sqrt {16-8}}{2}\end {cases} \quad \begin{cases} -1<x< 1 \\ x \neq 0 \\ x(3x+4)=0\end {cases}

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x \neq 0 \\ x_{\frac 12}=\frac {-4\pm 2\sqrt {2}}{2}\end {cases} \quad \begin{cases} -1<x< 1 \\ x \neq 0 \\ x=0 \quad \lor \quad x = -\frac 43\end {cases}

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x \neq 0 \\ x_{\frac 12}=-2\pm \sqrt 2\end {cases} \quad \begin{cases} -1<x< 1 \\ x \neq 0 \\ x=0 \quad \lor \quad x = -\frac 43\end {cases}

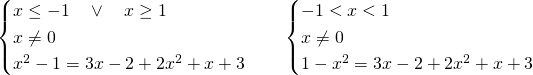
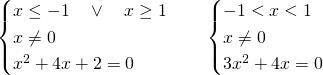
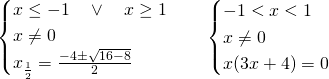
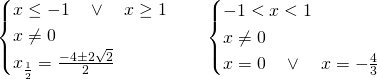
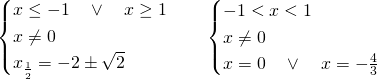
Il primo sistema ammetterà come soluzione solo x=-2-\sqrt 2, mentre il secondo sarà impossibile.

 

 

(Questa pagina è stata visualizzata da 112 persone)

Lascia un commento