Samuele scrive: Equazione con valore assoluto

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Equazioni con valore assoluto

Corpo del messaggio:
1)\frac { \left|x^2+3\right|}{\left|x-1\right|}-\left|x-2\right|=0

 

Risposta dello staff

Svolgiamo senza introdurre troppi arzigogoli, notando solo che x^2+3 è un binomio sempre positivo, e che quindi il suo valore assoluto è assolutamente superfluo.

Risolviamo quindi tre sistemi sulla positività dei 2 valori assoluti:

x-1 \geq 0 \iff x \geq 1

x-2 \geq 0 \iff x \geq 2

 

1 2
—- ++++ +++ +++ +++
—- —– —- +++ +++
++++ —- —- ++++ ++++

 

 

\begin{cases}x<1 \\ \frac { x^2+3}{1-x}-(2-x)=0 \end{cases} \quad \begin{cases}1 \leq x \leq 2 \\ \frac { x^2+3}{x-1}-(2-x)=0 \end{cases} \quad \begin{cases}x>2 \\ \frac { x^2+3}{x-1}-(x-2)=0 \end{cases}

\begin{cases}x<1 \\ x^2+3-(2-x)(1-x)=0 \end{cases} \quad \begin{cases}1 \leq x \leq 2 \\ x^2+3-(2-x)(x-1)=0 \end{cases} \quad \begin{cases}x>2 \\ x^2+3-(x-2)(x-1)=0 \end{cases}

\begin{cases}x<1 \\ x^2+3-2+2x+x-x^2=0 \end{cases} \quad \begin{cases}1 \leq x \leq 2 \\ x^2+3-2x+2+x^2-x=0 \end{cases} \quad \begin{cases}x>2 \\ x^2+3-x^2+x+2x-2=0 \end{cases}

\begin{cases}x<1 \\ 3x=-1 \end{cases} \quad \begin{cases}1 \leq x \leq 2 \\ 2x^2-3x+5=0 \end{cases} \quad \begin{cases}x>2 \\ 3x=-1 \end{cases}

\begin{cases}x<1 \\ x=-\frac 13 \end{cases} \quad \begin{cases}1 \leq x \leq 2 \\ x_{\frac 12}=\frac {3 \pm \sqrt {9-40}}{4} \end{cases} \quad \begin{cases}x>2 \\ x=-\frac 13 \end{cases}

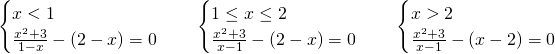
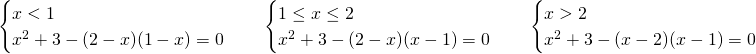
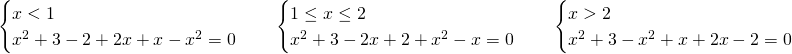
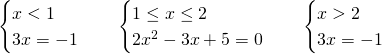
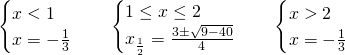
Notiamo quindi che il terzo sistema era superfluo, in quanto si poteva notare subito che il prodotto dei valori assoluti è uguale al valore assoluto del prodotto, e, quindi, primo e terzo sistema avrebbero avuto lo stesso procedimento.

Il secondo sistema non ammette soluzione poichè il \Delta risulta essere negativo.

 

Quindi l’equazione ammetterà come soluzione: x= -\frac 13.

(Questa pagina è stata visualizzata da 126 persone)

Lascia un commento