Traccia
![]()
Svolgimento
Per svolgere questa equazione dovremo considerare separatamente due casi, ovvero studiare il caso in cui il valore assoluto sia positivo e/o negativo e svolgere i calcoli singolarmente.
Studiamo prima la positività del modulo:
Senza svolgere tutti i calcoli, avremo che:
![]()
Quindi avremo che:
![]()
![]()
Studiamo i due sistemi:
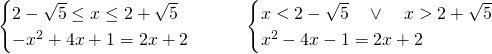
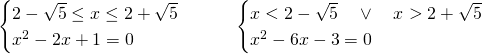
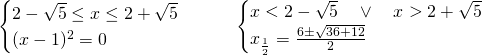
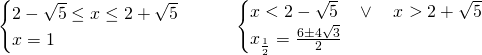
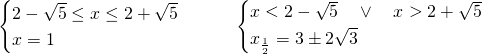
Di queste 3 soluzioni, solo due verificano le condizioni:
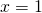 è accettabile
è accettabile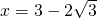 non è accettabile
non è accettabile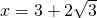 è accettabile
è accettabile
Altri esercizi simili:
- Esercizio 1 Valori assoluti: equazioni in cui compaiono valori assoluti
- Esercizio 2 Valori assoluti: equazioni in cui compaiono valori assoluti
- Esercizio 3 Valori assoluti: equazioni in cui compaiono valori assoluti
- Esercizio 4 Valori assoluti: equazioni in cui compaiono valori assoluti
- Esercizio 5 Valori assoluti: equazioni in cui compaiono valori assoluti
- Esercizio 6 Valori assoluti: equazioni in cui compaiono valori assoluti
- Esercizio 7 Valori assoluti: equazioni in cui compaiono valori assoluti
- Esercizio 8 Valori assoluti: equazioni in cui compaiono valori assoluti
(Questa pagina è stata visualizzata da 165 persone)