QUESTIONARIO
- Sia
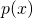 un polinomio di grado n. Si dimostri che la sua derivata n-esima è
un polinomio di grado n. Si dimostri che la sua derivata n-esima è 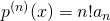 dove
dove 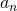 è il coefficiente di
è il coefficiente di 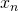 .
. - Siano ABC un triangolo rettangolo in A, r la retta perpendicolare in B al piano del triangolo e P un punto di r distinto da B. Si dimostri che i tre triangoli PAB, PBC, PCA sono triangoli rettangoli.
- Sia
 la retta di equazione
la retta di equazione 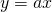 tangente al grafico di
tangente al grafico di 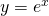 . Quale è la misura in gradi e primi sessagesimali dell’angolo che la retta
. Quale è la misura in gradi e primi sessagesimali dell’angolo che la retta  forma con il semiasse positivo dell’asse delle ascisse?
forma con il semiasse positivo dell’asse delle ascisse? - Si calcoli con la precisione di due cifre decimali lo zero della funzione
![Rendered by QuickLaTeX.com f(x)=\sqrt[3] x +x^3-1](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-b5a18fc5f7927f6c22e87c06d6347a3c_l3.png) . Come si può essere certi che esiste un unico zero?
. Come si può essere certi che esiste un unico zero? - Sia
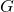 il grafico di una funzione
il grafico di una funzione 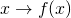 con
con 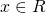 . Si illustri in che modo è possibile stabilire se
. Si illustri in che modo è possibile stabilire se 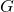 è simmetrico rispetto alla retta
è simmetrico rispetto alla retta 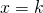 .
. - Si trovi l’equazione cartesiana del luogo geometrico descritto dal punto
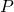 di coordinate
di coordinate 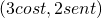 al variare di t,
al variare di t, 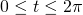 .
. - Per la ricorrenza della festa della mamma, la sig.ra Luisa organizza una cena a casa sua, con le sue amiche che hanno almeno una figlia femmina. La sig.ra Anna è una delle invitate, e perciò ha almeno una figlia femmina. Durante la cena, la sig.ra Anna dichiara di avere esattamente due figli. Si chiede: qual è la probabilità che anche l’altro figlio della sig.ra Anna sia femmina? Si argomenti la risposta.
- Se
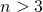 e
e 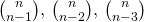 sono in progressione aritmetica, qual è il valore di n?
sono in progressione aritmetica, qual è il valore di n? - Si provi che non esiste un triangolo ABC con
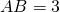 ,
,  e
e 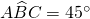 . Si provi altresì che se
. Si provi altresì che se 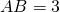 ,
,  e
e 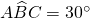 , allora esistono due triangoli che soddisfano queste condizioni.
, allora esistono due triangoli che soddisfano queste condizioni. - Si consideri la regione delimitata da
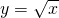 , dall’asse x e dalla retta
, dall’asse x e dalla retta 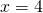 .
.
L’integrale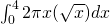 fornisce il volume del solido:
fornisce il volume del solido:
a) generato da R nella rotazione intorno all’asse x;
b) generato da R nella rotazione intorno all’asse y;
c) di base R le cui sezioni con piani perpendicolari all’asse x sono semicerchi di raggio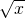 ;
;
d) nessuno di questi.
(Questa pagina è stata visualizzata da 9 persone)