Si consideri la regione delimitata da ![]() , dall’asse x e dalla retta
, dall’asse x e dalla retta ![]() e si calcoli il volume del solido che essa genera ruotando di un giro completo intorno all’asse y.
e si calcoli il volume del solido che essa genera ruotando di un giro completo intorno all’asse y.
Bisognerà calcolare il volume ottenuto ruotando la regione considerata intorno all’asse delle ordinate.
Tale volume può essere calcolato come la differenza tra:
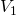 : volume del cilindro di raggio 4 e altezza 2
: volume del cilindro di raggio 4 e altezza 2 : volume del solido di rotazione ottenuto facendo ruotare la funzione
: volume del solido di rotazione ottenuto facendo ruotare la funzione  intorno all’asse
intorno all’asse 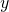 nell’intervallo
nell’intervallo ![Rendered by QuickLaTeX.com [0;2]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-2cdd0e45fe74350b68b51fcf0a4c9ce9_l3.png) .
.
![]()
![]()
Quindi:
![]()
Altri hanno visualizzato anche:
- Quesito 1 Scientifico 2010
- Quesito 2 Scientifico 2010
- Quesito 3 Scientifico 2010
- Quesito 4 Scientifico 2010
- Quesito 5 Scientifico 2010
- Quesito 6 Scientifico 2010
- Quesito 7 Scientifico 2010
- Quesito 8 Scientifico 2010
- Quesito 9 Scientifico 2010
- Quesito 10 Scientifico 2010
(Questa pagina è stata visualizzata da 7 persone)