In un libro si legge: “se per la dilatazione corrispondente a un certo aumento della temperatura un corpo si allunga (in tutte le direzioni) di una certa percentuale (p.es. 0,38%), esso si accresce in volume in proporzione tripla (cioè dell’1,14%), mentre la sua superficie si accresce in proporzione doppia (cioè di 0,76%)”. È così? Si motivi esaurientemente la risposta.
Possiamo scrivere la formula della dilatazione lineare di un corpo sotto la formula:
![]()
dove ![]() è la dilatazione percentuale.
è la dilatazione percentuale.
Se la dilatazione percentuale è molto piccola (quindi anche ![]() è molto minore di
è molto minore di ![]() ) nelle formule dell’area e del volume possiamo trascurare le potenze di
) nelle formule dell’area e del volume possiamo trascurare le potenze di ![]() superiori alla prima.
superiori alla prima.
Quindi avremo:
![]() .
.
Trascurando il termine quadratico e otteniamo:
![]() .
.
Stesso discorso per il volume:
![]() .
.
Quindi le due dilatazioni percentuali risultano:
- per la superficie:
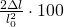
- per il volume:
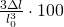
Altri esercizi simili
- Quesito 1 P.N.I. 2013
- Quesito 2 P.N.I. 2013
- Quesito 3 P.N.I. 2013
- Quesito 4 P.N.I. 2013
- Quesito 5 P.N.I. 2013
- Quesito 6 P.N.I. 2013
- Quesito 7 P.N.I. 2013
- Quesito 8 P.N.I. 2013
- Quesito 9 P.N.I. 2013
- Quesito 10 P.N.I. 2013
(Questa pagina è stata visualizzata da 17 persone)