Francesca scrive: Equazioni

Una studentessa scrive:

Nell’ equazione $2kx^2+(m-1)x+k+2m=0$ , k è diverso da 0, trova k e m sapendo che la somma delle soluzioni è uguale al loro prodotto e che una soluzione vale 2.

Risposta dello staff

Per risolvere questo bisognerà risolvere un sistema imponendo le condizioni che:

$-\frac ba = \frac ca$
$x=2$

Andiamo a risolvere il sistema:

$\begin {cases} -\frac {m-1}{2k} =\frac {k+2m}{2k} \\ 8k+2m-2+k+2m=0 \end {cases}$

$\begin {cases} 1-m =k+2m \\ 9k+4m-2=0 \end {cases}$

$\begin {cases} k+3m=1 \\ 9k+4m=2 \end {cases}$

$\begin {cases} k=1-3m \\ 9(1-3m)+4m=2 \end {cases}$

$\begin {cases} k=1-3m \\ 9-27m+4m=2 \end {cases}$

$\begin {cases} k=1-3m \\ -23m=7 \end {cases}$

$\begin {cases} k=1-3 \cdot (-\frac{7}{23}) \\ m=-\frac{7}{23} \end {cases}$

$\begin {cases} k=1+\frac{21}{23} \\ m=-\frac{7}{23} \end {cases}$

$\begin {cases} k=\frac{44}{23} \\ m=-\frac{7}{23} \end {cases}$

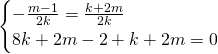
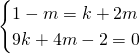
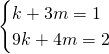
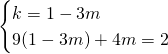
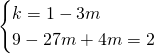
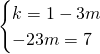
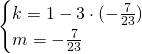
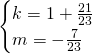
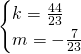
(Questa pagina è stata visualizzata da 376 persone)

Matebook

La matematica spiegata passo passo

Francesca scrive: Equazioni

Risposta dello staff

Lascia un commento Annulla risposta