Laura scrive: Esercizio equazioni

Oggetto: Equazioni

Corpo del messaggio:
Sono due esercizi

Determina i valori di 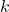$k$ in modo che l’equazione 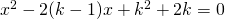$x^2-2(k-1)x+k^2+2k=0$ abbia radici reali.

Affinchè abbia radici reali, basterà imporre la positività del $\Delta$ .

$\Delta=b^2-4ac=4(k-1)^2-4(k^2+2k)=4k^2-8k+4-4k^2-8k=-16k+4.$

Quindi dovremo studiare:

$-16k+4 \geq 0 \Rightarrow 16k \leq 4 \Rightarrow k \leq \frac 14.$

Determina per quale valore del parametro 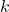$k$ k l’equazione 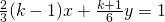$\frac 23 (k-1)x+ \frac {k+1}{6}y=1$ ammette come soluzione la coppia $x=6 \quad \wedge \quad y=4$ .

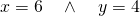Sostituiamo i valori delle incognite date dalla traccia nell’equazione, così da ottenere:

$\frac 23 (k-1)6+ \frac {k+1}{6}4=1$

$4k-4+ \frac 23 (k+1)=1$

$12k-12+ 2k+2=3$

$14k=3+10$

$14k=13$

$k=\frac {13}{14}.$

(Questa pagina è stata visualizzata da 102 persone)

Matebook