Oggetto: Disequazioni con moduli
![]()
![]()
Studiamo due casi:
![Rendered by QuickLaTeX.com \[\begin{cases} x > 0 \\ \frac {x -x^2}{x}<0 \end{cases} \quad \quad \begin{cases} x < 0 \\ \frac {-x -x^2}{x}<0\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-0cc248c3a2a480c3e3e428a482574a24_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > 0 \\ 1-x<0 \end{cases} \quad \quad \begin{cases}x < 0 \\ \-1-x<0\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-fbf4b5f1783ae26b85f3063449260a84_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > 0 \\ x>1 \end{cases} \quad \quad \begin{cases} x < 0 \\ \x>-1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-7584eb6de7bb851c11649b62542c578c_l3.png)
Il primo sistema ammetterà come soluzione ![]() , mentre il secondo
, mentre il secondo ![]() .
.
Studiamo due casi:
![Rendered by QuickLaTeX.com \[\begin{cases} x > \frac 32 \\ \frac {1}{2x-3}<3 \end{cases} \quad \quad \begin{cases} x < \frac 32 \\ \frac {1}{3-2x}<3 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-73e05f86808f7ffc695a35ec54d75cce_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > \frac 32 \\ \frac {1}{2x-3}-3<0 \end{cases} \quad \quad \begin{cases} x < \frac 32 \\ \frac {1}{3-2x}-3<0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-33a0d6bf4cb5cc202736dbde25f1d1ad_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > \frac 32 \\ \frac {1-6x+9}{2x-3}<0 \end{cases} \quad \quad \begin{cases} x < \frac 32 \\ \frac {1-9+6x}{3-2x}<0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-4a796f9b145ef8ca19ded4b4634be16e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > \frac 32 \\ -6x+10<0 \end{cases} \quad \quad \begin{cases} x < \frac 32 \\ 6x-8<0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-e6e918ca7b95c1233f8ca90216bfe0a7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > \frac 32 \\ x>\frac 53 \end{cases} \quad \quad \begin{cases} x < \frac 32 \\ x<\frac 43 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-af9d5e6c08a7eb0ea46af5baeab1dfb1_l3.png)
Il primo sistema ammetterà come soluzione ![]() , mentre il secondo
, mentre il secondo ![]() .
.
Studiamo due casi:
![Rendered by QuickLaTeX.com \[\begin{cases} x > 2 \\ \frac {2}{x+3}<\frac {3}{x-2 } \end{cases} \quad \quad \begin{cases} x < 2 \\ \frac {2}{x+3}<\frac {3}{2-x } \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-3239f8bf9a17af76f9e51545b84dced2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > 2 \\ \frac {2}{x+3}-\frac {3}{x-2 }<0 \end{cases} \quad \quad \begin{cases} x < 2 \\ \frac {2}{x+3}-\frac {3}{2-x }<0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-a000773437cc02fccc03cdb0d6484e7a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > 2 \\ \frac {2x-4-3x-9}{(x+3)(x-2)}<0 \end{cases} \quad \quad \begin{cases} x < 2 \\ \frac {4-2x-3x-9}{(x+3)(2-x)}<0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-b7ff071f20206af0e3af0c841a7aee63_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > 2 \\ \frac {-x-13}{(x+3)(x-2)}<0 \end{cases} \quad \quad \begin{cases} x < 2 \\ \frac {-5x-5}{(x+3)(2-x)}<0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-c9d85b87752ca817c84e7da746277691_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > 2 \\ \frac {x+13}{x+3}>0 \end{cases} \quad \quad \begin{cases} x < 2 \\ \frac {5x+5}{x+3}>0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-4aa85bdbd0215bc2b87b84493ce99422_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x > 2 \\ x<-13 \quad \lor \quad x>-3 \end{cases} \quad \quad \begin{cases} x < 2 \\ x<-3 \quad \lor \quad x>-1 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-738a68bf6ed7d2d6b3fa0da3b84a554e_l3.png)
Quindi, il primo sistema è verificato per ![]() , mentre il secondo per
, mentre il secondo per ![]()
Studieremo 3 casi:
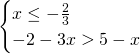
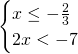
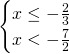
Che ammetterà come soluzione ![]() .
.
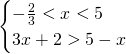
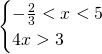
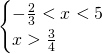
Che ammetterà come soluzione ![]() .
.
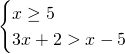
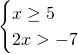
Che ammetterà come soluzione ![]() .
.
Unendo le tre soluzioni otteniamo: ![]() .
.



Le soluzioni sono ambedue accettabili.
(Questa pagina è stata visualizzata da 443 persone)
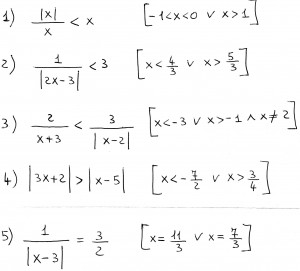
L’esercizio n. 4 si poteva anche risolvere elevando ambo i membri al quadrato e poi risolvendo la disequazione di secondo grado?
Distinti saluti
Chiaramente si. Ma non sapendo se chi affronta l’esercizio ha già studiato le disequazioni di secondo grado, ho preferito risolvere tutto con disequazioni di primo grado.
In merito all’esercizio n.1, vorrei sapere se è corretto risolverlo nel seguente modo:
Essendo nel 1° sistema x>0 la seconda disequazione si poteva semplificare in
x/x1 per cui il 1° sistema ha come soluzione x>1.
Invece nel 2°sistema, siccome x<0, si ha:
-x/x-1 per cui il 2° sistema ha come soluzione -1<x<0. Unendo le due soluzioni si ottiene il risutato finale.
Non ho capito il ragionamento… scusa ma non riesco a capire il significato di x/x1…
In merito al 1° esercizio riscrivo le disequazioni che forse non sono visualizzate bene:
Nel 1° sistema la seconda disequazione si poteva semplificare in
x/x minore di x cioè x maggiore di 1 per cui il 1° sistema ha come soluzione x>1
Invece nel 2°sistema,……:
-x/x minore di x cioè x maggiore di meno 1 per cui il secondo sistema ha come soluzione -1<x<0.
Unendo le due soluzioni si ottiene il risutato finale.
Si si…è esattamente quello che ho fatto… ma se hai visto bene mancava il pezzo iniziale nella seconda disequazione….
Lo rendo visibile così vedrai che è svolto esattamente nello stesso modo.
Prima ho tolto il modulo, e poi semplificato.
Riguardo al 2°esercizio, si poteva anche riscriverlo nella forma:
Modulo di 2x-3 maggiore di 1/3 e quindi risolvere
2x-3 minore di meno 1/3 e 2x-3 maggiore di 1/3 senza fare i sistemi.
Grazie
Si. Però se fai una cosa del genere, poi devi stare attento a ricordarti ( non è questo il caso), che nel caso fosse uscito come risultato accettabile anche x=2/3, sarebbe stato da escludere…
Se tu consideri solo modulo di 2x-3 maggiore di 1/3 rischi (ripeto, non è questo il caso) di considerare una soluzione che renderebbe la disequazione priva di significato.