Alberto scrive: Continuità e derivabilità di una funzione

Pubblicato il da Lo StaffLascia un commento
0

Oggetto:

Corpo del messaggio:
Studiare la continuità e la derivabilita’ della funzione:

f(x)= x^2e^{-\left|x^2 - 2\right|}

 

Risposta dello staff

f(x)=\begin{cases} x^2e^{2-x^2}, & \mbox{se } x< -\sqrt 2 \quad \lor \quad x > \sqrt 2 \\ x^2e^{x^2-2}, & \mbox{se } -\sqrt 2 \leq x \leq \sqrt 2 \end{cases}

 

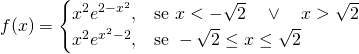
Essendo un prodotto di una funzione razionale intera e di una esponenziale non ci sono problemi di continuità. La funzione sarà continua in tutto \mathbb{R}.

Studiamo invece la derivabilità e distinguiamola in 2 casi:

f'(x)=\begin{cases} 2xe^{2-x^2 }-2x^3e^{2-x^2}, & \mbox{se } x< -\sqrt 2 \quad \lor \quad x > \sqrt 2 \\ 2xe^{x^2-2 }+2x^3e^{x^2-2} , & \mbox{se } -\sqrt 2 \leq x \leq \sqrt 2 \end{cases}

f'(x)=\begin{cases} 2xe^{2-x^2 }(1-x^2), & \mbox{se } x< -\sqrt 2 \quad \lor \quad x > \sqrt 2 \\ 2xe^{x^2-2 }(1+x^2) , & \mbox{se } -\sqrt 2 \leq x \leq \sqrt 2 \end{cases}

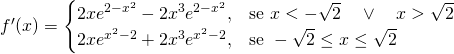
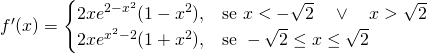
Calcoliamo i limiti:

\lim_{x \to -\sqrt 2^-}f'(x)=-2\sqrt 2e^0(1-2)=2\sqrt 2

\lim_{x \to -\sqrt 2^+}f'(x)=-2\sqrt 2e^0(1+2)=-6\sqrt 2

Analogamente avremo:

\lim_{x \to \sqrt 2^+}f'(x)=2\sqrt 2e^0(1-2)=2\sqrt 2

\lim_{x \to \sqrt 2^-}f'(x)=2\sqrt 2e^0(1+2)=6\sqrt 2

(Questa pagina è stata visualizzata da 73 persone)

Lascia un commento