Chiara scrive: Circonferenze 3

Pubblicato il da EdoLascia un commento
0

Dato il punto P(-1;3) , dopo aver determinato le coordinate dei punti Q edR, di intersezione delle due circonferenze di equazioni x^2 +y^2 -4x -2y+4=0  e  x^2+y^2 -4y=0, calcola l’area del triangolo PQR.

Risposta dello staff

Allora, innanzitutto calcoliamo i punti di intersezione tra le circonferenze:

\begin{cases}x^2 +y^2 -4x -2y+4=0 \\ x^2+y^2 -4y=0 \end{cases}

\begin{cases}x^2 +y^2 -4x -2y+4=0 \\ 4x-2y-4=0\end{cases}

\begin{cases}x^2 +y^2 -4x -2y+4=0 \\ y=2x-2\end{cases}

\begin{cases} x^2 +4x^2-8x+4-4x -4x+4+4=0 \\ y=2x-2 \end{cases}

\begin{cases} 5x^2 -16x+12=0 \\ y=2x-2 \end{cases}

x_{\frac 12}=\frac {16 \pm \sqrt {256-240}}{10}=\frac {16 \pm \sqrt {16}}{10}=\frac {16 \pm 4}{10}

x_1=\frac 65

x_2=2

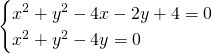
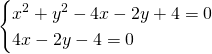
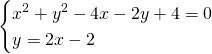
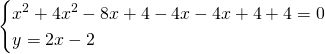
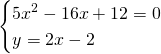
da cui:

y_1=\frac 25

y_2=2

Quindi il triangolo sarà formato da:

P(-1;3)

Q(\frac 65; \frac 25

R(2;2)

L’area di un triangolo si calcola con il determinante di:

A=\frac 12 \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix}

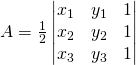
da cui:

A=\frac 12 \begin{vmatrix} -1 & 3 & 1 \\ \frac 65 & \frac 25 & 1 \\ 2 & 2 & 1 \end{vmatrix} =\frac 12 \left| -\frac 25 +6 +\frac {12}{5} +2 -\frac {18}{5} -\frac 45\right|=\frac 12 \cdot \frac {28}{5}=\frac {14}{5}

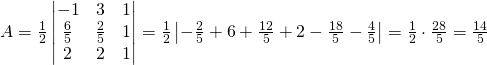
(Questa pagina è stata visualizzata da 69 persone)

Lascia un commento