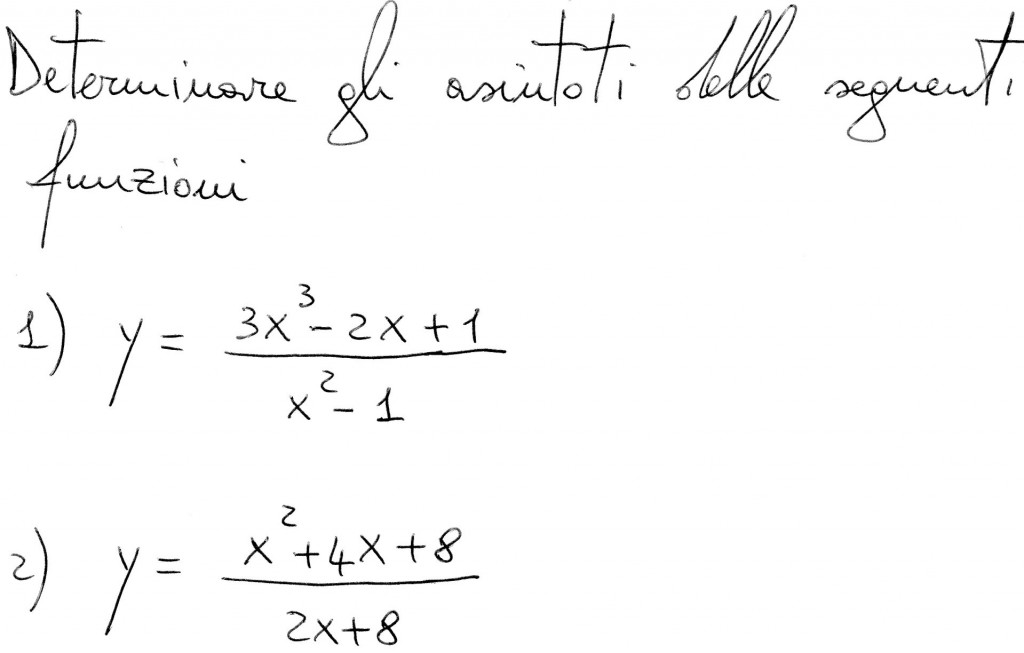Leandro scrive: Asintoti

Oggetto: Asintoti

Corpo del messaggio:

Riscriviamo meglio la funzione:

$y=\frac{(3x^2-3x+1)(x+1)}{(x-1)(x+1)}$

Da qui ricaviamo che l’unico asintoto verticale è:

$x=1$

Asintoto orizzontale non è presente in quanto il grado del numeratore è maggiore del grado del denominatore.

Verifichiamo quindi l’esistenza di asintoti obliqui del tipo $y=mx+q$ , dove:

$m=\lim_{x \to \pm \infty} \frac{3x^3-2x+1}{x^3-x}=3$

$q=\lim_{x \to \pm \infty} \frac{3x^3-2x+1}{x^2-1}-3x=$

$=\lim_{x \to \pm \infty} \frac{3x^3-2x+1-3x^3+3x}{x^2-1}=0$

L’asintoto obliquo è quindi:

$y=3x$

Riscriviamo la funzione:

$y=\frac{x^2+4x+8}{2(x+4)}$

Da qui ricaviamo che l’unico asintoto verticale è:

$x=-4$

Asintoto orizzontale non è presente in quanto il grado del numeratore è maggiore del grado del denominatore.

Verifichiamo quindi l’esistenza di asintoti obliqui del tipo $y=mx+q$ , dove:

$m=\lim_{x \to \pm \infty} \frac{x^2+4x+8}{2x^2+8x}=\frac 12$

$q=\lim_{x \to \pm \infty} \frac{x^2+4x+8}{2x+8}-\frac 12x=$

$=\lim_{x \to \pm \infty} \frac{x^2+4x+8-x^2-4x}{2x+8}=0$

L’asintoto obliquo è quindi:

$y=\frac 12x$

(Questa pagina è stata visualizzata da 48 persone)

Matebook