Problemi di argomento vario
- In una frazione il numeratore supera il denominatore di 3. Trovare la frazione sapendo che la somma della frazione stessa con il suo reciproco è
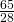
![]()
![]()
sostituendo a ![]() otteniamo l’equazione fratta:
otteniamo l’equazione fratta:
![]()
![]()
![]()
![]()
![]()
![]()
Al solito si può risolvere o come trinomio speciale o come equazione di secondo grado.
Come trinomio speciale, i due numeri la cui somma è 3 e il prodotto è -28 sono 7 e -4. Quindi:
![]() ; da cui le soluzioni per il denominatore sono 4 e -7, mentre per il numeratore sarebbero 7 e -4.
; da cui le soluzioni per il denominatore sono 4 e -7, mentre per il numeratore sarebbero 7 e -4.
Come equazione di secondo grado:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Le coppie quindi sono quelle viste sopra.
Altri esercizi simili:
- Esercizio 1 Problemi di secondo grado
- Esercizio 2 Problemi di secondo grado
- Esercizio 3 Problemi di secondo grado
- Esercizio 4 Problemi di secondo grado
- Esercizio 5 Problemi di secondo grado
- Esercizio 6 Problemi di secondo grado
- Esercizio 7 Problemi di secondo grado
- Esercizio 8 Problemi di secondo grado
- Esercizio 9 Problemi di secondo grado
- Esercizio 10 Problemi di secondo grado
(Questa pagina è stata visualizzata da 478 persone)