PROBLEMA 1
Sia ABCD un quadrato di lato 1, P un punto di AB e la circonferenza di centro P e raggio AP. Si prenda sul lato BC un punto Q in modo che sia il centro di una circonferenza passante per C e tangente esternamente a .

1. Se 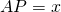, si provi che il raggio di 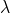in funzione di è dato da .
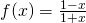2. Riferito il piano ad un sistema di coordinate Oxy, si tracci, indipendentemente dalle limitazioni poste ad dal problema geometrico, il grafico di 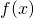. La funzione 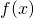è invertibile? Se sì, quale è il grafico della sua inversa?
3. Sia 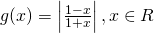; quale è l’equazione della retta tangente al grafico di nel punto 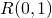? E nel punto ? Cosa si può dire della tangente al grafico di nel punto ?
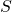4. Si calcoli l’area del triangolo mistilineo ROS, ove l’arco RS appartiene al grafico di 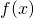o, indifferentemente, di .

 

 

 

Altri hanno visualizzato anche:

• Problema 1 PNI 2010
• Problema 1 Scientifico 2010
• Problema 2 PNI 2010
• Problema 2 Scientifico 2010
• Quesiti P.N.I. 2010
• Quesiti Scientifico 2010

(Questa pagina è stata visualizzata da 6 persone)