Oggetto: soluzione di un esercizio
Corpo del messaggio:
ciao potresti svolgermi questo esercizio: determinare i minimi e massimi relativi della funzione x^2. la radice 4x+5 e anche della funzione ln(x^2+1) fratti 1+x^2 ti ringrazio!!!
Non è molto chiara la traccia, ma cerchiamo di capire la richiesta…
Dovrebbero essere 3 funzioni differenti.
Analizziamo caso per caso:
In questo caso, senza bisogno di grossi calcoli, sapendo che questa l’equazione di una parabola, possiamo subito dire che il minimo relativo e anche assoluto è rappresentato dal vertice della parabola stessa ovvero:
![]() .
.
Non avrà invece massimi relativi ne assoluti…
Qui possiamo subito dire che essendo la funzione una radice quadrata, allora ammetterà minimo nel punto in cui questa sarà annullata, mentre non ammetterà massimo in quanto è radice di una funzione lineare, con coefficiente dell’incognita positivo e quindi sempre crescente.
![]() .
.
Qui c’è un discorso più complicato, in quanto bisognerà studiare necessariamente la derivata prima. Per fortuna notiamo che il dominio coincide con tutto l’insieme dei numeri reali, e quindi non ci sono limitazioni ne sull’argomento del logaritmo, ne sul denominatore.
![]()
![]()
Studiamo la positività della derivata prima:
- N1:
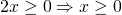
- N2:
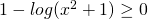
![]()
![]()
![]()
![]() .
.
- D:
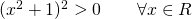 .
.
| |
|
|||
| —— | —– | +++++++ | —– | ——- |
Quindi vediamo come questa funzione ammetterà 2 massimi e 1 minimo relativo in:
![]()
![]()
![]() .
.
(Questa pagina è stata visualizzata da 152 persone)