Andrea scrive: Esercizio di algebra

Pubblicato il da Lo StaffLascia un commento
0

Oggetto:

Corpo del messaggio:

image (1)

 

 

\begin{cases} \frac {x^4-6x^2+9}{x-1} \leq 0 \\ \frac {\left|x-8 \right|-1}{\sqrt{x+2}}>0 \end{cases}

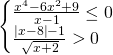
Notiamo subito che la prima disequazione è pressochè immediata, essendo il numeratore un quadrato di binomio, che si annulla per x^2=3 \iff x=\pm \sqrt 3, mentre il denominatore è positivo per x \geq 1.

Per la seconda disequazione, bisognerà imporre l’esistenza della radice e studiare solo il numeratore.

Il sistema diventa quindi:

\begin{cases} x=\pm \sqrt 3 \quad \lor \quad x<1 \\ x>-2 \\ \left|x-8\right| >1\end {cases}

\begin{cases} x=\pm \sqrt 3 \quad \lor \quad x<1 \\ x>-2 \\ \x-8<-1 \quad \lor\quad x-8 >1\end {cases}

\begin{cases} x=\pm \sqrt 3 \quad \lor \quad x<1 \\ x>-2 \\ \x<7 \quad \lor\quad x >9\end {cases}

 

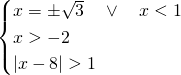
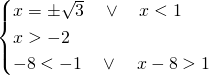
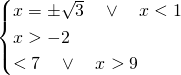
Dal grafico si evince che la soluzione è:

    \[-2<x<1 \quad \lor \quad x=-\sqrt 3.\]

 

 

(Questa pagina è stata visualizzata da 105 persone)

Lascia un commento