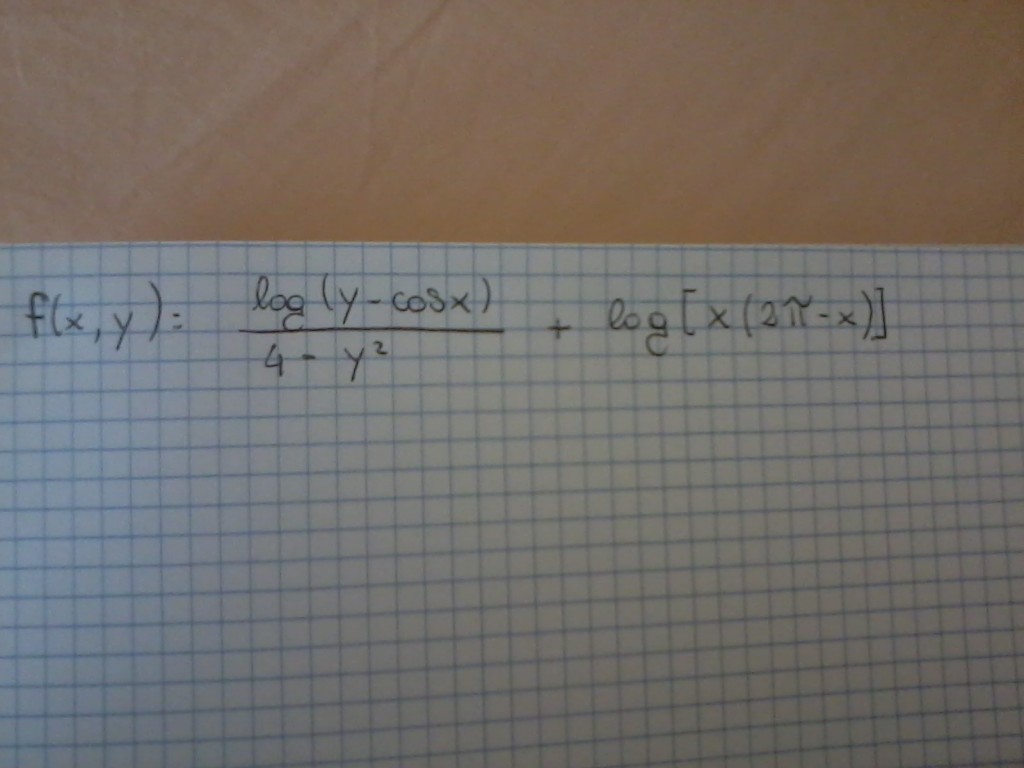Sofia scrive: Dominio funzione a 2 variabili

Oggetto: dominio funzione a 2 variabili

Corpo del messaggio:

$f(x,y)=\frac {log(y-cosx)}{4-y^2} +log\left [x\left(2 \pi-x \right) \right]$

Per studiare il dominio dobbiamo considerare tutti i fattori che formano la funzione, quindi:

$\begin{cases} y-cosx >0 \\ 4-y^2 \neq 0 \\ x(2\pi-x) >0\end{cases}$

Analizziamo caso per caso:

$y-cosx>0 \rightarrow y>cosx$

$4-y^2 \neq 0 \rightarrow y^2 \neq 4 \rightarrow y \neq \pm2$

$x(2\pi-x) >0 \rightarrow x(x-2\pi)<0 \rightarrow 0<x<2pi$

Il sistema diventa quindi:

$\begin{cases} y>cosx \\ y \neq \pm 2 \\ 0<x<2\pi\end{cases}$

Dalla prima notiamo che $y >-1$ ; per $y\geq 1$ non ci sono mai problemi, eccetto $y=2$ .

$Dom(f)= \{ (x,y) \in \mathbb{R}^2 \, \, \mbox { t.c. } y> cosx \wedge 0<x<2 \pi \wedge y >- 1 \wedge y \neq 2\}$

(Questa pagina è stata visualizzata da 107 persone)

Matebook