Piero scrive: problema geometrico grafico

Pubblicato il da Lo Staff1 commento
0

Oggetto: problema geometrico grafico

Corpo del messaggio:
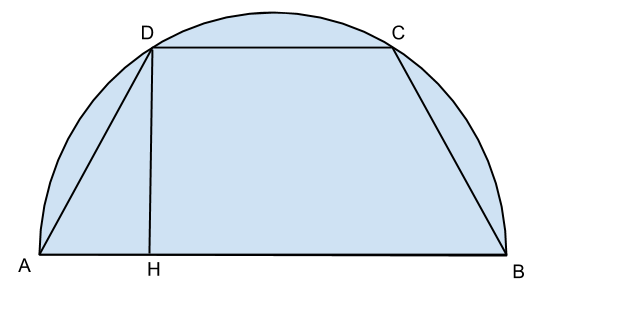
inscrivere ad una semicirconferenza di raggio r, un trapezio isoscele con perimetro 2kr.

trapezio isoscele semi circonferenza

 

Risposta dello staff

 

Chiamando con

AH=x

BH=2r-x

Di sicuro avremo che:

DC=2r-2x

Troviamo il lato obliquo sapendo che un triangolo inscritto in una semicirconferenza è sicuramente retto, e quindi possiamo sfruttare il teorema di Euclide:

AD=\sqrt{AH \cdot AB}=\sqrt{2rx}

Ora che abbiamo tutti e 4 i lati, troviamo il valore dell’incognita sapendo il perimetro del trapezio:

2p=2r+2\sqrt{2rx}+2r-2x=2kr

2r+2\sqrt{2rx}+2r-2x=2kr

2\sqrt{2rx}=2kr+2x-4r

\sqrt{2rx}=kr+x-2r

2rx=k^2r^2+x^2+4r^2+2krx-4kr^2-4rx

k^2r^2+x^2+4r^2+2krx-4kr^2-4rx-2rx=0

x^2+2krx-6rx+k^2r^2+4r^2-4kr^2=0

x^2+2rx(k-3)+r^2(k^2-4k+4)=0

x_{\frac 12}=\frac {-2r(k-3) \pm \sqrt {4r^2(k-3)^2-4r^2(k^2-4k+4)}}{2}

x_{\frac 12}=\frac {-2r(k-3) \pm \sqrt {4r^2k^2-24kr^2+36r^2-4r^2k^2+16kr^2-16r^2}}{2}

x_{\frac 12}=\frac {-2r(k-3) \pm \sqrt {-8kr^2+20r^2}}{2}

x_{\frac 12}=\frac {-2r(k-3) \pm 2r\sqrt {5-2k}}{2}

x_{\frac 12}= -r(k-3) \pm r\sqrt {5-2k}

x_{\frac 12}=r\left( 3-k \pm \sqrt {5-2k}\right)

Studiamo quindi quali sono i valori di k che rendono vera la soluzione:

3-k - \sqrt{5-2k} \geq 0

3-k \geq \sqrt{5-2k}

\begin{cases} 3-k \geq 0 \\ 5-2k \geq 0 \\ 9-6k+k^2 \geq 5-2k\end{cases}

\begin{cases} k \leq 3 \\ k \leq \frac 52 \\ k^2-4k+4 \geq 0 \end{cases}

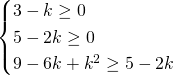
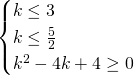
Essendo il terzo un quadrato di binomio è verificato per k \leq \frac 52

3-k + \sqrt{5-2k} \geq 0

\sqrt{5-2k} \geq k-3

\begin{cases} k-3 \geq 0 \\ 5-2k \geq k^2-6k+9 \end{cases} \qquad \qquad \begin{cases} k-3 < 0 \\ 5-2k \geq 0 \end{cases}

\begin{cases} k \geq 3 \\ k^2-4k+4 \leq 0\end{cases} \qquad \qquad \begin{cases} k < 3 \\ k \leq \frac 52 \end{cases}

\begin{cases} k \geq 3 \\ (k-2)^2 \leq 0\end{cases} \qquad \qquad \begin{cases} k < 3 \\ k \leq \frac 52 \end{cases}

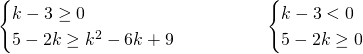
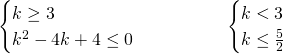
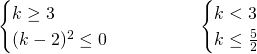
Il primo sistema ammetterà un’unica soluzione k=2, il secondo ammetterà k \leq \frac 52

Unendo le due soluzioni otteniamo che la soluzione sarà:

k \leq \frac 52.

Notiamo però che, essendo il perimetro uguale a 2kr ed il diametro, ovvero la base maggiore, uguale ad r, allora k deve essere necessariamente maggiore di 1 e quindi:

1 <k \leq \frac 52

 

 

 

 

(Questa pagina è stata visualizzata da 126 persone)

Un pensiero riguardo “Piero scrive: problema geometrico grafico”

  1. C’è un errore. Il testo parla di trapezio isoscele circoscritto, non iscritto in una semicirconferenza.
    Poi con il metodo algebrico sembra tutto molto complicato, non si può risolvere con il metodo grafico e l’aiuto della geometria analitica?

Lascia un commento