Carmen scrive: Compito di matematica

Oggetto: Problema

Corpo del messaggio:

L’equazione sarà:

$\frac{x^2}{25}+\frac{y^2}{49}=1$

Le coordinate di P e Q le troviamo sostituendo 0 al posto della x e quindi:

$y^2=49$

$y=\pm 7$

$P(0;7)$

$Q(0;-7)$

Ricaviamo invece le coordinate di A e B:

$\begin{cases} y= \frac 75 x \\ \frac{x^2}{25}+\frac{y^2}{49}=1\end{cases}$

$\begin{cases} y= \frac 75 x \\ \frac{x^2}{25}+\frac{\frac{49}{25}x^2}{49}=1 \end{cases}$

$\begin{cases} y= \frac 75 x \\ \frac{x^2}{25}+\frac{x^2}{25}=1\end{cases}$

$\begin{cases} y= \frac 75 x \\ 2x^2=25\end{cases}$

$\begin{cases} y= \frac 75 x \\ x=\pm \frac 52 \sqrt 2\end{cases}$

$\begin{cases} y=\pm \frac 72 \sqrt 2 \\ x=\pm \frac 52 \sqrt 2\end{cases}$

$A(\frac 52 \sqrt 2;\frac 72 \sqrt 2)$

$B(-\frac 52 \sqrt 2;-\frac 72 \sqrt 2)$

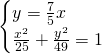
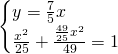
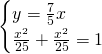
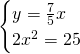
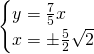
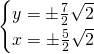
Ricaviamo i coefficienti angolari dei segmenti:

$m_{AP}=\frac{\frac 52 \sqrt 2}{\frac 72 \sqrt 2-7}$

$m_{PB}=\frac{\frac 52 \sqrt 2}{\frac 72 \sqrt 2+7}$

$m_{AQ}=\frac{\frac 52 \sqrt 2}{\frac 72 \sqrt 2+7}$

$m_{QB}=\frac{\frac 52 \sqrt 2}{\frac 72 \sqrt 2-7}$

come vediamo, le rette sono a due a due parallele, e quindi il quadrilatero in questione è un parallelogrammo.

(Questa pagina è stata visualizzata da 59 persone)

Matebook