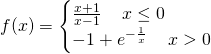
Risposta dello staff
Studiamo il dominio della funzione.
Nel primo tratto l’unico valore da escludere sarebbe ![]() , ma non appartiene al tratto. Nel secondo sarebbe da escludere
, ma non appartiene al tratto. Nel secondo sarebbe da escludere ![]() , ma anche qui non appartiene al dominio.
, ma anche qui non appartiene al dominio.
Di conseguenza avremo che il dominio è tutto ![]()
Studiamo la positività dei due tratti:
![]()
![]()
Quindi, nel tratto considerato avremo che:
![]()
![]()
![]()
Studiamo il secondo tratto:
![]()
![]()
![]()
Ma quindi, nel tratto considerato non si verificherà mai e unendo le due soluzioni, l’unica cosa che si modifica è:
![]()
Studiamo i limiti negli estremi del dominio ed in 0 per la continuità:
![]()
![]()
![]()
![]()
Quindi in ![]() la funzione è continua.
la funzione è continua.
Studiamo ora la derivata prima:
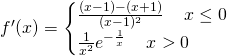
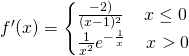
E’ facile capire che per ![]() la derivata prima è negativa, mentre per
la derivata prima è negativa, mentre per ![]() è sempre positiva.
è sempre positiva.
(Questa pagina è stata visualizzata da 48 persone)
Un pensiero riguardo “Ginevra scrive: Matematica 1.1”