Oggetto: Matematica
Corpo del messaggio:
Risposta dello staff
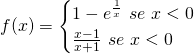
Come vediamo il dominio sarà tutto ![]() , perchè se nel primo tratto escluderemmo lo 0, già escluso cmq, nel secondo tratto escluderemmo
, perchè se nel primo tratto escluderemmo lo 0, già escluso cmq, nel secondo tratto escluderemmo ![]() , ma li le x sono considerate solo positive.
, ma li le x sono considerate solo positive.
Studiamo la positività:
![]()
![]()
![]()
![]()
Quindi, nel primo tratto è sempre positiva.
![]()
![]()
Quindi, mettendo a sistema con tutta la funzione otteniamo che:
![]()
![]()
![]()
Studiamo i limiti agli estremi:
![]()
![]()
![]()
![]()
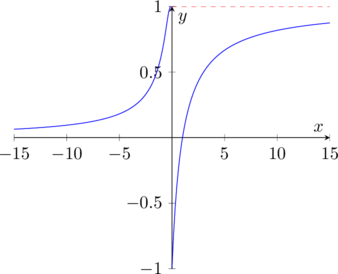
Quindi avremo due asintoti orizzontali, e notiamo che la funzione in 0 non è continua.
Studiamo ora la derivata prima:
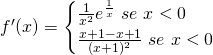
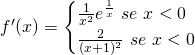
Quindi, la funzione, nei due singoli intervalli, è sempre crescente.
(Questa pagina è stata visualizzata da 46 persone)
