Esercizio 3 Equazioni irrazionali contenenti radicali quadratici 2

Traccia

$\sqrt{x+6}-\sqrt{x+1}=\sqrt{2x-5}$

Svolgimento

$\sqrt{x+6}=\sqrt{x+1}+\sqrt{2x-5}$

Essendo le radici già isolate, possiamo elevare subito al quadrato dopo aver verificato le condizioni di esistenza.

$\begin {cases} x+6 \geq 0 \\ x+1 \geq 0 \\ 2x-5 \geq 0 \end{cases}$

$\begin {cases} x \geq -6 \\ x \geq -1 \\ x \geq \frac 52 \end{cases}$

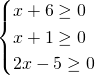
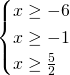
Quindi, affinchè siano verificate entrambe deve succedere che:

$x \geq \frac {5}{2}$ .

Eleviamo ora tutto al quadrato:

$x+6=x+1+2x-5+2\sqrt{(x+1)(2x-5)}$

$2-2x=2\sqrt{(x+1)(2x-5)}$

$1-x=\sqrt{(x+1)(2x-5)}$

Elevando nuovamente al quadrato otteniamo:

$1-2x+x^2=2x^2-3x-5$

$x^2-x-6=0$

Da questa avremo due soluzioni:

$x=-2$ non accettabile, e

$x=3$ accettabile.

Altri esercizi simili

(Questa pagina è stata visualizzata da 406 persone)

2 pensieri riguardo “Esercizio 3 Equazioni irrazionali contenenti radicali quadratici 2”

lo svolgimento mi sembra errato…

Salve,

Volevo avere un chiarimento su un passaggio specifico
##################
Eleviamo ora tutto al quadrato:

x+6=x+1+2x-5+2\sqrt{(x+1)(2x-5)}

2-2x=2\sqrt{(x+1)(2x-5)}
##################

Non riesco a capire come diventa 2 – 2x.
A me viene 10 – 2x.
Grazie
Saluti

Mattia Abbate

Matebook