Per il progetto di una piscina, un architetto si ispira alle funzioni f e g definite, per tutti gli x reali, da:
![\[f(x) = x^3 - 16x \quad \quad \mbox { e } \quad \quad g(x)= sen \frac {\pi}{2} x.\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-98ee5af5253fe8a6c16331e68e3e7d61_l3.png "Rendered by QuickLaTeX.com")
- Si studino le funzioni
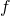e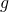 
e se ne disegnino i rispettivi grafici in un conveniente sistema di riferimento cartesiano 
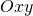. Si considerino i punti del grafico di 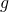a tangente orizzontale la cui ascissa è compresa nell’intervallo [–10; 10] e se ne indichino le coordinate. - L’architetto rappresenta la superficie libera dell’acqua nella piscina con la regione R delimitata dai grafici 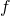di e di 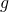sull’intervallo [0; 4]. Si calcoli l’area di R.
- Ai bordi della piscina, nei punti di intersezione del contorno di R con le rett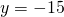e
e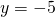 
, l’architetto progetta di collocare dei fari per illuminare la superficie dell’acqua. Si calcolino le ascisse di tali punti (è sufficiente un’approssimazione a meno di 
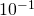). - In ogni punto di R a distanza
dall’asse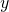 
, la misura della profondità dell’acqua nella piscina è data da 
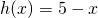. Quale sarà il volume d’acqua nella piscina? Quanti litri d’acqua saranno necessari per riempire la piscina se tutte le misure sono espresse in metri?
Altri esercizi simili
- Problema 1 P.N.I. 2011
- Problema 1 Scientifico 2011
- Problema 2 P.N.I. 2011
- Problema 2 Scientifico 2011
- Quesiti P.N.I. 2011
- Quesiti Scientifico 2011
(Questa pagina è stata visualizzata da 30 persone)