Sia ![]() la funzione definita sull’insieme R dei numeri reali da
la funzione definita sull’insieme R dei numeri reali da
![]()
dove a e b sono due reali che si chiede di determinare sapendo che ![]() ammette un massimo nel punto d’ascissa 4 e che
ammette un massimo nel punto d’ascissa 4 e che ![]() .
.
- Si provi che
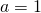 e
e 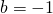 .
. - Si studi su R la funzione
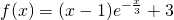 e se ne tracci il grafico
e se ne tracci il grafico 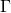 nel sistema di riferimento
nel sistema di riferimento 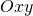 .
. - Si calcoli l’area della regione di piano del primo quadrante delimitata da
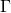 , dall’asse
, dall’asse 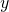 e dalla retta
e dalla retta 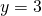 .
. - Il profitto di una azienda, in milioni di euro, è stato rappresentato nella tabella sottostante designando con xi l’anno di osservazione e con yi il corrispondente profitto.
| Anno | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 1,97 | 3,02 | 3,49 | 3,71 | 3,80 | 3,76 | 3,65 |
Si cerca una funzione che spieghi il fenomeno dell’andamento del profitto giudicando accettabile una funzione ![]() definita su
definita su ![]() se per ciascun
se per ciascun ![]() , oggetto dell’osservazione, si ha:
, oggetto dell’osservazione, si ha: ![]() . Si verifichi, con l’aiuto di una calcolatrice, che è accettabile la funzione
. Si verifichi, con l’aiuto di una calcolatrice, che è accettabile la funzione ![]() del punto 2 e si dica, giustificando la risposta, se è vero che, in tal caso, l’evoluzione del fenomeno non potrà portare a profitti inferiori ai 3 milioni di euro.
del punto 2 e si dica, giustificando la risposta, se è vero che, in tal caso, l’evoluzione del fenomeno non potrà portare a profitti inferiori ai 3 milioni di euro.
Altri esercizi simili
- Problema 1 P.N.I. 2011
- Problema 1 Scientifico 2011
- Problema 2 P.N.I. 2011
- Problema 2 Scientifico 2011
- Quesiti P.N.I. 2011
- Quesiti Scientifico 2011
(Questa pagina è stata visualizzata da 28 persone)