Siano ![]() e
e ![]() le funzioni definite da
le funzioni definite da ![]() e
e ![]() .
.
- Fissato un riferimento cartesiano
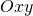 , si disegnino i grafici di
, si disegnino i grafici di 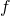 e di
e di 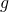 e si calcoli l’area della regione R che essi delimitano tra
e si calcoli l’area della regione R che essi delimitano tra 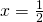 e
e 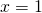 .
. - La regione R, ruotando attorno all’asse
 , genera il solido S e, ruotando attorno all’asse
, genera il solido S e, ruotando attorno all’asse 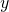 , il solido T. Si scrivano, spiegandone il perché, ma senza calcolarli, gli integrali definiti che forniscono i volumi di S e di T.
, il solido T. Si scrivano, spiegandone il perché, ma senza calcolarli, gli integrali definiti che forniscono i volumi di S e di T. - Fissato
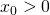 , si considerino le rette
, si considerino le rette  e
e  tangenti ai grafici di
tangenti ai grafici di 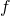 e di
e di 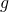 nei rispettivi punti di ascissa
nei rispettivi punti di ascissa 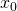 . Si dimostri che esiste un solo
. Si dimostri che esiste un solo 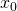 per il quale
per il quale  e
e  sono parallele. Di tale valore
sono parallele. Di tale valore 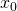 si calcoli un’approssimazione arrotondata ai centesimi.
si calcoli un’approssimazione arrotondata ai centesimi. - Sia
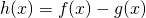 . Per quali valori di
. Per quali valori di  la funzione
la funzione 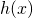 presenta, nell’intervallo chiuso
presenta, nell’intervallo chiuso 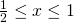 il minimo e il massimo assoluti? Si illustri il ragionamento seguito.
il minimo e il massimo assoluti? Si illustri il ragionamento seguito.
Altri esercizi simili
- Problema 1 P.N.I. 2012
- Problema 1 Scientifico 2012
- Problema 2 P.N.I. 2012
- Problema 2 Scientifico 2012
- Quesiti P.N.I. 2012
- Quesiti Scientifico 2012
(Questa pagina è stata visualizzata da 16 persone)