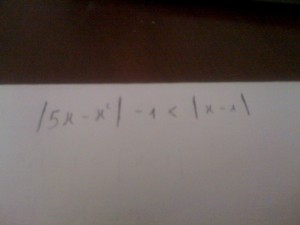Oggetto:
Corpo del messaggio:
![]()
Analizziamo singolarmente i due valori assoluti:
Da qui si evince che dovremo studiare più sistemi e poi unire le soluzioni:

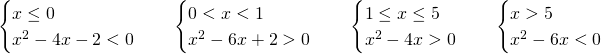
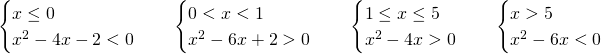
![]()
![]()
![]()
![]() .
.
Quindi le soluzioni dei singoli sistemi sono:

- impossibile
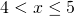
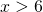
La soluzione della disequazione iniziale è l’unione delle 4 soluzioni.
(Questa pagina è stata visualizzata da 150 persone)