rispondete con una certa urgenza per favore
Come si vede, ![]() è una funzione irrazionale con radice di indice pari, quindi il dominio sarà formato da tutti i valori della x che rendono positivo il radicando, mentre
è una funzione irrazionale con radice di indice pari, quindi il dominio sarà formato da tutti i valori della x che rendono positivo il radicando, mentre ![]() è una funzione razionale intera, e quindi sarà verificata
è una funzione razionale intera, e quindi sarà verificata ![]() .
.
Calcoliamo la positività del radicando:
![]()
![]()
![]()
Avremo quindi:
![]()
Ovviamente, intersecando i due, otterremo proprio che ![]() .
.
Per il punto b) dobbiamo notare alcune cose:
- la funzione
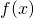 è sempre positiva, tocca l’asse delle ascisse nei punti
è sempre positiva, tocca l’asse delle ascisse nei punti 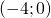 e
e 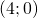 , e l’asse delle ordinate in
, e l’asse delle ordinate in 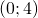 .
. - la funzione
 è anch’essa sempre positiva, ma varrà
è anch’essa sempre positiva, ma varrà 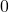 per
per 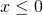 e varrà
e varrà 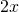 per
per 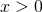 .
.
Quindi ![]() sarà maggiore di
sarà maggiore di ![]() dal punto
dal punto ![]() fino all’altro punto di intersezione, che avrà come ascissa un valore positivo compreso tra 0 e 4.
fino all’altro punto di intersezione, che avrà come ascissa un valore positivo compreso tra 0 e 4.
Calcoliamolo imponendo l’uguaglianza tra le due funzioni, ricordando che, per x positive, ![]() :
:
![]()
![]()
![]()
![]()
![]()
Quindi, avremo che:
![]()
(Questa pagina è stata visualizzata da 147 persone)
