Corpo del messaggio:
verificare che il triangolo di vertici A (3;2) B (6;1) C(5;4) è isoscele e determinare il perimetro e area.
Scrivere l’equazione di una retta per il punto A (3-1/2) e parallela alla retta R 3x-2y=4 e perpendicolare alla retta y=-2x-4.
Rappresenta le seguenti rette R:2x+y+6=0 S=3x-4y+1=0.
Aiuto sono esercizi da svolgere per superare il test di recupero per lunedì grazie
Risposta dello staff
Ciao, da quanto leggo credo che sto svolgendo questi esercizi in ritardo, ma capita che anche noi andiamo in ferie ogni tanto!!! 🙂
A parte questo, ecco la soluzione:
- Per vedere se il triangolo è isoscele, la cosa più facile da fare è calcolare la lunghezza dei singoli segmenti e verificare che due di questi siano uguali:
![]()
![]()
![]()
Quindi il triangolo ABC è isoscele su base AC.
Il perimetro sarà:
![]()
Per calcolare l’area ci sono più modi. Analizziamo uno di questi; calcoliamo l’altezza del triangolo vedendolo come distanza dal vertice B al punto medio della base.
![]()
![]()
Calcoliamo BM:
![]()
Quindi l’area sarà:
![]()
- Questa traccia non è molto chiara perchè non sarà possibile avere una retta che passa per quel punto e sia nello stesso tempo parallela ad una retta e perpendicolare all’altra.
Ma possiamo calcolare sicuramente singolarmente le due richieste:
Il coefficiente angolare della prima retta è:
![]()
quindi, essendo parallela, sfruttiamo la formula e calcoliamo:
![]()
![]()
da cui:
![]() .
.
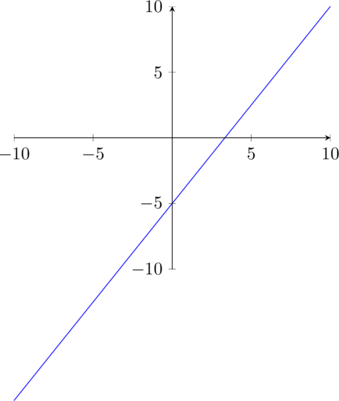
Nella seconda retta il coefficiente angolare è:
![]()
Quindi il coefficiente angolare affinchè la retta sia perpendicolare sarà:
![]()
Usando la stessa formula otteniamo:
![]()
![]()
da cui:
![]() .
.
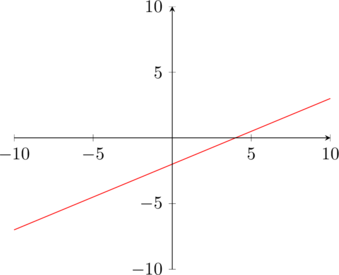
(Questa pagina è stata visualizzata da 224 persone)
ottimo e veloce
Grazie per il commento!!! Scusa di nuovo per il ritardo nello svolgimento.
recupero superato grazie!!!!