Data
![\[f(x)=\frac {2x^2+5x+3}{2x+3}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-66d68ddb26bae257c36b61995df5327a_l3.png "Rendered by QuickLaTeX.com")
- calcolare il limite destro e il limite sinistro in
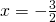
- dire se
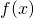ha massimi relativi.
Risposta dello staff
Notiamo che il numeratore si può scrivere come:
Quindi, in realtà, 
non appartiene al dominio, ma il limite destro e il limite sinistro calcolato in sarà:
![\[\lim_{x \to -\frac 32^{\pm}} f(x)=\lim_{x \to -\frac 32^{\pm}} (x+1)=-\frac 12\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-04a3a93f2f5bf91f5249fb6a6fc281fa_l3.png "Rendered by QuickLaTeX.com")
Non è proprio bellissima come scrittura, ma rende l’idea del risultato.
Essendo il comportamento di questa funzione simile a quello di una retta (eccetto per il punto escluso da dominio) possiamo subito affermare che non ammetterà massimi relativi.
(Questa pagina è stata visualizzata da 52 persone)