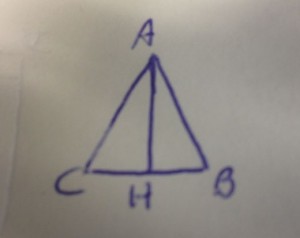
Risoluzione e spiegazione del seguente problema risolubile con il teorema di pitagora
- Il perimetro di un triangolo isoscele è di 64 cm e il lato supera di 5 cm i
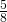 della base. Determinare le lunghezze dei lati e dell’altezza relativa alla base.
della base. Determinare le lunghezze dei lati e dell’altezza relativa alla base.
Dai dati e dal disegno otteniamo, ponendo ![]() :
:
![]()
![]()
Sostituendo quest’ultima nell’equazione del perimetro otteniamo:
![]() (ometto le unità di misura per comodità…)
(ometto le unità di misura per comodità…)
![]()
![]()
![]()
![]()
Da cui:
![]()
Per calcolare l’altezza relativa alla base sfruttiamo il teorema di Pitagora sul triangolo rettangolo formato dal lato e da metà della base (proprietà dei triangoli isosceli):
![]()
![]()
Altri esercizi simili:
- Problema 1
- Problema 2
- Problema 3
- Problema 4
- Problema 5
- Problema 6
- Problema 7
- Problema 8
- Problema 9
- Problema 10
(Questa pagina è stata visualizzata da 499 persone)