Problema 4

-3

Risoluzione e spiegazione del seguente problema risolubile con il teorema di pitagora

 

  1. In un trapezio rettangolo la base maggiore è doppia della minore e supera l’altezza di 10 m. Determinare la lunghezza del perimetro e l’area del trapezio sapendo che la somma dell’altezza e dei 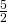\frac 5 2 della base minore è 26 m.

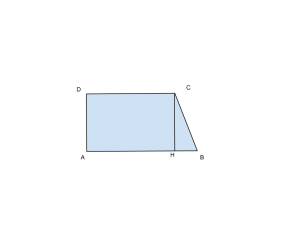
trapeziorettangoloaltezzabase

Dai dati e dal disegno, ponendo AB=x, AD=y, otteniamo:

DC=2x

DC=y+10 \mbox { m}

y+\frac 5 2 x=26 \mbox { m}

Dai risultati delle prime due equazioni otteniamo:

2x=y+10 (ometto le unità di misura per comodità…)

da cui:

y=2x-10

Sostituendo quest’ultima nella 3° equazione iniziale otteniamo:

2x-10+\frac 5 2 x=26

\frac {4x-20+5x}{2}=\frac {52}{2}

9x=52+20

9x=72

x=8 \mbox { m}

Quindi

y=2x-10 = (16-10)\mbox { m}=6 \mbox { m}

Di conseguenza, la base maggiore sarà:

DC=2x=16\mbox { m}

Per calcolare BC sfruttiamo il teorema di Pitagora sul triangolo BHC sapendo che il segmento HC risulterà essere proprio la metà della base maggiore; quindi

BC=\sqrt {BH^2+HC^2}

BC=\sqrt {6^2+8^2} \mbox { m} =\sqrt {36+64} \mbox { m} =\sqrt {100} \mbox { m}=10\mbox { m}

Perimetro e area saranno:

2p=(8+6+16+10) \mbox { m}=40 \mbox { m}

A=\frac 1 2 (8+16)*6 \mbox { m}^2=72 \mbox { m}^2

 

 

 

 

 

Altri esercizi simili:

 

 

(Questa pagina è stata visualizzata da 541 persone)

Lascia un commento