Risoluzione e spiegazione del seguente problema risolubile con il teorema di pitagora
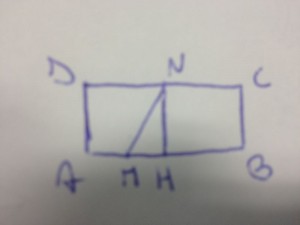
- Del rettangolo ABCD si conosce la base AB=64 cm e l’altezza BC=1 dm. Si prenda su AB un punto M e su CD un punto N in modo che sia DN=2 AM e che l’area del trapezio AMND sia 360 cm
 . Determinare il perimetro dei due trapezi AMND e MBCN.(Porre
. Determinare il perimetro dei due trapezi AMND e MBCN.(Porre 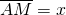 ).
).
Poniamo ![]() . Da questo e dai dati otteniamo:
. Da questo e dai dati otteniamo:
![]()
![]()
![]() .
.
Nel trapezio ![]() le due basi sono rappresentate proprio da
le due basi sono rappresentate proprio da ![]() e
e ![]() , quindi sostituendo con le incognite appena inserite, otteniamo:
, quindi sostituendo con le incognite appena inserite, otteniamo:
![]() (ometto le unità di misura per comodità…)
(ometto le unità di misura per comodità…)
![]()
![]()
![]()
![]()
![]()
Ora ci serve solo calcolare il lato obliquo ![]() , che possiamo calcolare con il teorema di Pitagora sul triangolo rettangolo
, che possiamo calcolare con il teorema di Pitagora sul triangolo rettangolo ![]() . Per calcolare
. Per calcolare ![]() , basta vedere che possiamo vederlo come differenza di segmenti:
, basta vedere che possiamo vederlo come differenza di segmenti:
![]()
Quindi, per il th di Pitagora avremo:
![]()
![]()
Così adesso possiamo calcolare i 2 perimetri:
![]()
![]()
Altri esercizi simili:
- Problema 1
- Problema 2
- Problema 3
- Problema 4
- Problema 5
- Problema 6
- Problema 7
- Problema 8
- Problema 9
- Problema 10
(Questa pagina è stata visualizzata da 458 persone)