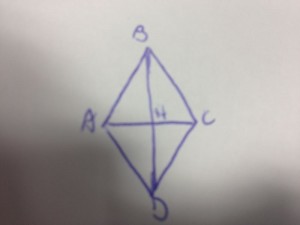
Risoluzione e spiegazione del seguente problema risolubile con il teorema di pitagora
In un rombo ABCD la diagonale BD è i ![]() della diagonale AC e si sa che
della diagonale AC e si sa che ![]() .Trovare il perimetro del rombo.
.Trovare il perimetro del rombo.
Dal disegno e dai dati otteniamo, ponendo ![]() :
:
![]()
![]()
Sostituendo la prima nella seconda, otteniamo:
![]()
![]()
![]()
![]()
![]()
![]() .
.
Per trovare il perimetro del rombo basta trovare la lunghezza di un lato, sapendo che le semidiagonali formano con il lato un triangolo rettangolo; sfruttando così il teorema di Pitagora otteniamo:
![]()
quindi il perimetro sarà:
![]() .
.
Altri esercizi simili:
- Problema 1
- Problema 2
- Problema 3
- Problema 4
- Problema 5
- Problema 6
- Problema 7
- Problema 8
- Problema 9
- Problema 10
(Questa pagina è stata visualizzata da 443 persone)