Problema 9

0

Risoluzione e spiegazione del seguente problema risolubile con il teorema di pitagora

 

 

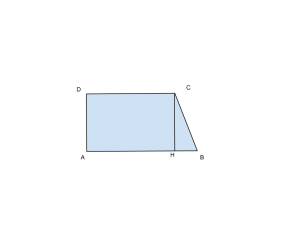
Nel trapezio rettangolo ABCD , AB è la base maggiore e AD il lato perpendicolare alle basi.  Si sa che AD=\frac 3 4 AB e CD=\frac {11}{12}AD; la somma delle basi è 54 cm. Dopo aver determinato la base maggiore AB, determinare l’area del trapezio e il perimetro.

 

trapeziorettangoloaltezzabase

 

Dai dati e dal disegno, ponendo AB=x, AD=y, CD=z, otteniamo:

y=\frac 3 4 x

z=\frac {11}{12}y

x+z=54 \mbox { cm}

Analizzando le prime tre otteniamo:

z=\frac {11}{12} \frac 3 4 x= \frac {33}{48}x

da cui otteniamo nell’ultima:

x+\frac {33}{48}x=54

\frac {48+33}{48}x=54

\frac {81}{48}x=54

x=\frac {48}{81} 54= 32 \mbox { cm}

y=\frac 3 4 x = \frac 3 4 32 \mbox { cm}=24 \mbox { cm}.

z=\frac {11}{12} y =\frac {11}{12} 24 \mbox { cm}=22 \mbox { cm}

L’area sarà:

A=\frac 1 2 (AB+CD)AD=\frac 1 2 (32 +22)24 \mbox { cm}^2=648 \mbox { cm}^2.

Per calcolare il perimetro ci serve il lato obliquo BC che calcoleremo con il teorema di Pitagora sul triangolo rettangolo BCH, dove il segmento BH lo otteniamo come differenza tra le due basi:

BH=AB-CD=(32-22) \mbox { cm} = 10 \mbox { cm}

BC=\sqrt {BH^2+CH^2}=\sqrt {10^2+24^2} \mbox { cm}= \sqrt {100+576} \mbox { cm} = \sqrt {676} \mbox { cm}=26 \mbox { cm}.

2p=(32+26+22+24) \mbox { cm}=104 \mbox { cm}

 

 

 

 

Altri esercizi simili:

 

 

(Questa pagina è stata visualizzata da 400 persone)

Lascia un commento