Problema 6

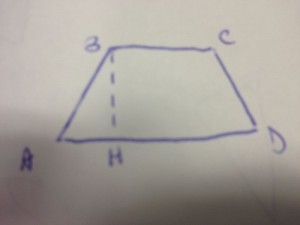
Risoluzione e spiegazione del seguente problema risolubile con il teorema di pitagora

In un trapezio isoscele la somma delle basi è 32 cm e la maggiore è i 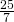$\frac {25} 7$ della minore; si sa che l’altezza è di 12 cm. Determinare l’area e il perimetro del trapezio.

Dai dati e dal disegno, ponendo $AD=x, BC=y$ , otteniamo:

$x+y=32 \mbox { cm}$

$x=\frac {25}{7} y$

$BH=12 \mbox { cm}$

Sostituendo la seconda nella prima otteniamo:

$\frac {25}{7}y+y=32$ (ometto le unità di misura per comodità…)

$\frac {25+7}{7}y=32$

$frac {32}{7}y=32$

$y=\frac {7}{32} 32=7 \mbox { cm}$

$x=\frac {25}{7} y=\frac {25}{7} 7 \mbox { cm}=25 \mbox { cm}$

L’area sarà quindi:

$A=\frac 1 2 (AD+BC)BH=\frac 1 2 (25+7)*12 \mbox { cm}^2=192 \mbox { cm}^2$

Per calcolare il perimetro ci serve il lato obliquo $AB=CD$ . Sfruttiamo il triangolo equilatero $ABH$ e, quindi, per applicare il teorema di Pitagora, bisogna prima calcolare $AH$ :