Oggetto: Problema geometria risolvibile con equazioni

Corpo del messaggio:
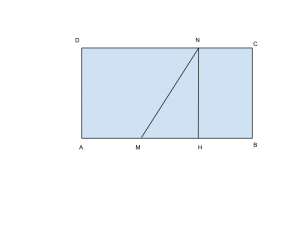
Del rettangolo ABCD si conosce la base AB=64 cm e l’altezza BC=1 dm. Prendi su AB un punto M e su CD un punto N in modo che sia DN=2AM e che l’area del trapezio AMND sia 360 cm. Determina il perimetro dei due trapezi AMND e MBCN. (poni AM = x) soluzione 108cm; 92cm

 

 

 

Come da traccia poniamo , così da avere

.

Sapendo che l’area del trapezio AMND sarà:

,

imponiamo l’uguaglianza:

.

Da cui ricaviamo:

.

Ci resta solo da trovare MN, che ricaviamo con la costruzione, prendendo H sul lato AB, del triangolo rettangolo MNH, sapendo che:

.

.

Ricaviamo ora i 2 perimetri:

 

 

 

(Questa pagina è stata visualizzata da 149 persone)