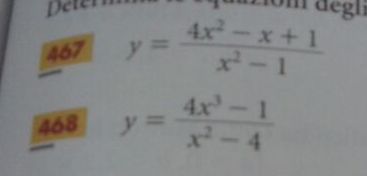Eleonora scrive: Equazione

Pubblicato il da Lo StaffLascia un commento
0

Corpo del messaggio:
Potreste aiutarmi a svolgere questi esercizi?Grazie in anticipo^^

Determina le equazioni degli eventuali asintoti delle seguenti funzioni …

IMG-20140207-WA0000

 

Risposta dello staff

y = \frac {4x^2-x+1}{x^2-1}

Per calcolare gli asintoti verticali, basterà verificare che, i limiti per i punti esclusi dal dominio, vadano a \infty.

In questo caso il dominio della funzione sarà:

D= \mathbb{R}- \{ \pm 1\}

Quindi, se ci fossero asintoti verticali, questi sarebbero proprio le rette x= \pm 1.

Calcoliamo i limiti, tralasciando lo studio dei segni:

    \[\lim_{x \to - 1} \frac {4x^2-x+1}{x^2-1}= \frac {6}{0}= \infty\]

    \[\lim_{x \to 1} \frac {4x^2-x+1}{x^2-1}= \frac {4}{0}= \infty\]

Essendo numeratore e denominatore dello stesso grado, possiamo subito affermare che ammetterà asintoto orizzontale:

    \[\lim_{x \to \infty} \frac {4x^2-x+1}{x^2-1}=\lim_{x \to \infty} \frac {4x^2(1-\frac {x}{4x^2}+\frac {1}{4x^2}}{x^2(1-\frac {1}{x^2}}= 4\]

Quindi y=4 sarà l’asintoto orizzontale di questa funzione.

 

y = \frac {4x^3-1}{x^2-4}

Per calcolare gli asintoti verticali, basterà verificare che, i limiti per i punti esclusi dal dominio, vadano a \infty.

In questo caso il dominio della funzione sarà:

D= \mathbb{R}- \{ \pm 2\}

Quindi, se ci fossero asintoti verticali, questi sarebbero proprio le rette x= \pm 2.

Calcoliamo i limiti, tralasciando lo studio dei segni:

    \[\lim_{x \to - 2} \frac {4x^3-1}{x^2-4}= \frac {-33}{0}= \infty\]

    \[\lim_{x \to 2} \frac {4x^3-1}{x^2-4}= \frac {31}{0}= \infty\]

Essendo il grado del numeratore superiore di uno rispetto al grado del denominatore, possiamo subito affermare che non ammetterà asintoto orizzontale, e che potrà esserci asintoto obliquo, di equazione y=mx+q. Calcoliamo m e q:

    \[m=\lim_{x \to \infty} \frac {4x^3-1}{x^2-4} \cdot \frac 1x=\lim_{x \to \infty} \frac {4x^3-1}{x^3-4x}= 4\]

    \[q=\lim_{x \to \infty} \frac {4x^3-1}{x^2-4} -4x=\lim_{x \to \infty} \frac {4x^3-1-4x^3+16x}{x^2-4}= 0\]

Quindi y=4x sarà l’asintoto obliquo di questa funzione.

 

 

(Questa pagina è stata visualizzata da 79 persone)

Lascia un commento