Oggetto: Dimostrazioni teoremi geometria
Corpo del messaggio:
Dato un triangolo isoscele ABC traccia, dagli estremi B e C della base, rispettivamente due semirette b e c formanti con BC angoli tra loro congruenti e interne agli angoli alla base del triangolo isoscele. Siano P e Q rispettivamente i punti in cui b interseca AC e c interseca AB. Dimostra che BQ congruente CP.
Risposta dello staff
Dato che le semirette formano angoli uguali avremo che:
e
, per differenza di angoli uguali.
Chiamando M il punto di intersezione tra b e c, avremo che il triangolo BMC è isoscele e di conseguenza
.
Da ciò avremo che i due triangoli BMQ e CMP sono congruenti avendo:
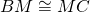
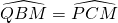
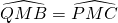perchè opposti al vertice.
E quindi saranno congruenti i due lati:
(Questa pagina è stata visualizzata da 288 persone)