Assunta scrive: esercizio 1

Pubblicato il da Edo1 commento
0

Data l’ellisse di equazione:

\frac{x^2}{25}+\frac{y^2}{9}=1

si trovi l’equazione della parabola avente per asse l’asse delle y, che interseca l’ellisse nel suo punto di intersezione con il semiasse negativo delle y e che passa per i fuochi F_1 e F_2 dell’ellisse.

Risposta dello staff

Sapendo che la parabola ha come asse l’asse delle ordinate, possiamo subito assumere che la parabola sia del tipo:

y=ax^2+c.

Ora, l’ellisse intersecherà il semiasse negativo delle y nel punto (0;-3).

Ricaviamo ora i due fuochi dell’ellisse:

F(\pm f;0)

dove f=\sqrt{25-9}=4

Quindi sappiamo che passa per (4;0) e per (-4;0).

Da queste due avremo che:

\begin{cases} -3=c \\ 0=16a+c \end{cases}

\begin{cases} -3=c \\ 0=16a-3 \end{cases}

\begin{cases} c=-3 \\ a= \frac {3}{16} \end{cases}

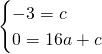
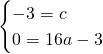
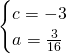
L’equazione della parabola sarà quindi:

y= \frac {3}{16} x^2-3

 

 

(Questa pagina è stata visualizzata da 93 persone)

Un pensiero riguardo “Assunta scrive: esercizio 1”

  1. Pingback: Assunta scrive: Esercizio con punti di circonferenza, ellisse e iperbole | Matebook

Lascia un commento