Traccia
![]()
Svolgimento
Questa equazione non è proprio immediata, ma bisognerà adottare un artificio, ovvero le formule parametriche:
![]()
![]() ,
,
dove ![]() .
.
Sostituendo il tutto nell’equazione iniziale otteniamo
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Usiamo le proprietà dei radicali doppi:
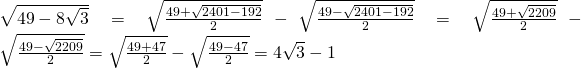 .
.
![]()
![]()
Altri esercizi simili:
- Esercizio 1 equazioni lineari in seno e coseno
- Esercizio 2 equazioni lineari in seno e coseno
- Esercizio 3 equazioni lineari in seno e coseno
- Esercizio 4 equazioni lineari in seno e coseno
- Esercizio 5 equazioni lineari in seno e coseno
- Esercizio 6 equazioni lineari in seno e coseno
- Esercizio 7 equazioni lineari in seno e coseno
- Esercizio 8 equazioni lineari in seno e coseno
- Esercizio 9 equazioni lineari in seno e coseno
- Esercizio 10 equazioni lineari in seno e coseno
- Esercizio 11 equazioni lineari in seno e coseno
- Esercizio 12 equazioni lineari in seno e coseno
- Esercizio 13 equazioni lineari in seno e coseno
- Esercizio 14 equazioni lineari in seno e coseno
- Esercizio 15 equazioni lineari in seno e coseno
(Questa pagina è stata visualizzata da 514 persone)
Esercizi svolti in modo perfettamente chiaro con spiegazione di ogni passaggio.Utilissimo, grazie.
Grazie, a volerVi porre una traccia?
Distinti saluti
Antonio