Oggetto: problema con le funzioni

Corpo del messaggio:
considerate quello in fondo alla pagina (l’ ultimo)
grazie

 

 

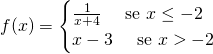
a) Calcoliamo i tre valori, considerando l’intervallo corrispondente:

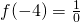• . Si capisce che questo valore non fa parte del dominio…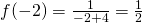
• 
• 
• 

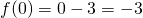
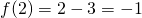
b) Il dominio, visto che la funzione è formata da una funzione razionale fratta e una razionale intera sarà proprio tutto R escluso il valore che annulla il denominatore, quindi:

.

Per il codominio, analizziamo subito che, la seconda funzione ammette come codominio . A questo dovremo unire il codominio della prima funzione.

Senza dover fare grossi calcoli notiamo che, nei suoi intervalli, la funzione è decrescente, che e che poco prima di arrivare a -4 assume tutti i valori negativi fino a .

Quindi il codominio della funzione sarà: .

c) Affinchè il punto (3;1) appartenga alla funzione deve verificarsi che ; ma come vediamo, , e quindi il punto non appartiene al grafico.F

 

 

(Questa pagina è stata visualizzata da 130 persone)