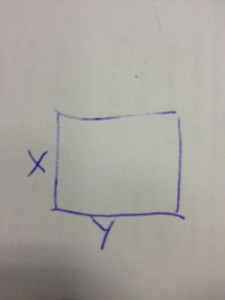
Soluzione e svolgimento del seguente problemi di geometria piana.
- Il rapporto fra le dimensioni di un rettangolo è
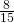 e l’area è 10,8 dm
e l’area è 10,8 dm . Trovare il perimetro.
. Trovare il perimetro.
Chiamiamo con ![]() e
e ![]() le dimensioni del rettangolo.
le dimensioni del rettangolo.
avremo che:
![]() ,
,
![]() .
.
Dalla prima otteniamo:
![]()
Dalla seconda:
![]() .
.
Sostituendo il valore della ![]() nella seconda equazione otteniamo:
nella seconda equazione otteniamo:
![]()
da cui:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Escludiamo a priori la soluzione negativa, in quanto un lato non potrà mai avere misura negativa…
Trovato ![]() , possiamo sostituire questo valore per trovare la
, possiamo sostituire questo valore per trovare la ![]() :
:
![]()
Quindi il perimetro sarà:
![]() .
.
Altri esercizi simili:
- Esercizi equazioni di secondo grado: Problema 1 di geometria piana
- Esercizi equazioni di secondo grado: Problema 2 di geometria piana
- Esercizi equazioni di secondo grado: Problema 3 di geometria piana
- Esercizi equazioni di secondo grado: Problema 4 di geometria piana
- Esercizi equazioni di secondo grado: Problema 5 di geometria piana
- Esercizi equazioni di secondo grado: Problema 6 di geometria piana
- Esercizi equazioni di secondo grado: Problema 7 di geometria piana
- Esercizi equazioni di secondo grado: Problema 8 di geometria piana
- Esercizi equazioni di secondo grado: Problema 9 di geometria piana
- Esercizi equazioni di secondo grado: Problema 10 di geometria piana
- Esercizi equazioni di secondo grado: Problema 11 di geometria piana
- Esercizi equazioni di secondo grado: Problema 12 di geometria piana
(Questa pagina è stata visualizzata da 1015 persone)