Soluzione e svolgimento del seguente problemi di geometria piana.
- Il perimetro di un rombo è cm 204 e una diagonale è i
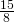 dell’altra. Calcolare l’area del rombo.
dell’altra. Calcolare l’area del rombo.
Chiamiamo con ![]() il lato del rombo e con
il lato del rombo e con ![]() e
e ![]() le diagonali del quadrilatero.
le diagonali del quadrilatero.
Dai dati otteniamo che:
![]()
![]()
Dalla prima equazione otteniamo:
![]() .
.
Ora dobbiamo sfruttare le proprietà del rombo: le diagonali si intersecano nel loro punto medio perpendicolarmente. Ciò significa che il rombo si divide in 4 triangoli rettangoli uguali tra di loro, dove le due semidiagonali sono i cateti e il lato del rombo è l’ipotenusa.
Sfruttando questo, la seconda equazione dei dati, e il teorema di Pitagora otteniamo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Escludiamo a priori la soluzione negativa in quanto un lato non può assumere misura negativa.
Calcoliamo quindi la diagonale maggiore:
![]()
Conoscendo le due diagonali possiamo così calcolare l’area:
![]()
Altri esercizi simili:
- Esercizi equazioni di secondo grado: Problema 1 di geometria piana
- Esercizi equazioni di secondo grado: Problema 2 di geometria piana
- Esercizi equazioni di secondo grado: Problema 3 di geometria piana
- Esercizi equazioni di secondo grado: Problema 4 di geometria piana
- Esercizi equazioni di secondo grado: Problema 5 di geometria piana
- Esercizi equazioni di secondo grado: Problema 6 di geometria piana
- Esercizi equazioni di secondo grado: Problema 7 di geometria piana
- Esercizi equazioni di secondo grado: Problema 8 di geometria piana
- Esercizi equazioni di secondo grado: Problema 9 di geometria piana
- Esercizi equazioni di secondo grado: Problema 10 di geometria piana
- Esercizi equazioni di secondo grado: Problema 11 di geometria piana
- Esercizi equazioni di secondo grado: Problema 12 di geometria piana
(Questa pagina è stata visualizzata da 812 persone)
Perdonate un dubbio:
il dato trovato (y=24) non è la semidiagonale del rombo? Non si dovrebbe moltiplicare per 2 (y=48), prima di calcolare la lunghezza della diagonale maggiore (e poi l’area)?
Grazie per l’attenzione.
Riveduto e corretto.
Grazie per averci fatto notare la svista.