Esercizi equazioni di secondo grado: Problema 12 di geometria piana

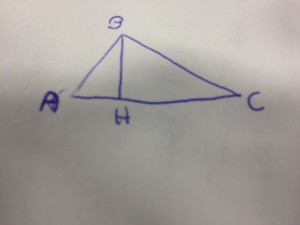
Soluzione e svolgimento del seguente problemi di geometria piana.

In un triangolo rettangolo un cateto è lungo cm 45 e la sua proiezione sull’ipotenusa è i 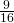$\frac {9}{16}$ della proiezione dell’altro cateto sull’ipotenusa. Trovare perimetro ed area del triangolo.

In base ai dati poniamo:

$\overline {AB}=45 \mbox { cm}$

$\overline{HC}=x$

$\overline {AH}=\frac {9}{16}x$ .

Per risolvere il problema dobbiamo sfruttare il teorema di Euclide:

$AB^2=AH*AC$

Ci manca trovare $AC$ , ma che possiamo trovare come somma delle due proiezioni; quindi:

$AC=AH+HC=\frac {9}{16}x +x=\frac {25}{16}x$

Sostituendo il tutto nell’equazione del Th di Euclide otteniamo:

$45^2=\frac {9}{16}x * \frac {25}{16}x$

Senza svolgere tutti i calcoli, possiamo riscrivere il tutto così:

$\frac {9*25}{16^2}x^2=45^2$

e, facendo la radice quadrata di ambo i membri otteniamo:

$\frac {3*5}{16} x = 45$

da cui:

$x=\frac {16}{15} 45=48$ .

Quindi:

$HC=48 \mbox { cm}$

$AH=\frac {9}{16} 48 \mbox { cm}=27 \mbox { cm}$

$AC=(48+27)\mbox { cm}=75 \mbox { cm}$

$BC$ lo possiamo trovare con il teorema di pitagora o con il teorema di Euclide…. Sfruttiamo il secondo, per rapidità di calcolo:

$BC^2=CH*AC=48*75 \mbox { cm}^2$

$BC=\sqrt {3600}\mbox { cm}=60\mbox { cm}$ .

Avendo ottenuto i 2 cateti e l’ipotenusa possiamo calcolare perimetro e area:

$2p= (45+60+75)\mbox { cm}=180 \mbox { cm}$

$A=\frac 1 2 (45*60) \mbox { cm}^2=1350 \mbox { cm}^2$

Altri esercizi simili:

(Questa pagina è stata visualizzata da 1040 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.