Soluzione e svolgimento del seguente problemi di geometria piana.
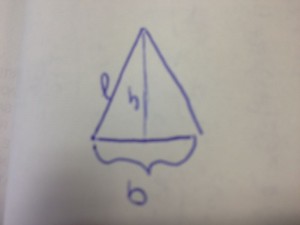
- In un triangolo isoscele la base supera di a l’altezza, mentre ciascuno dei due lati congruenti supera di a la base. Trovare il perimetro e l’area del triangolo.
Definiamo con ![]() la base, con
la base, con ![]() l’altezza e con
l’altezza e con ![]() i lati del triangolo isoscele. Dai dati otteniamo che:
i lati del triangolo isoscele. Dai dati otteniamo che:
![]()
![]() .
.
Dalle proprietà del triangolo isoscele dobbiamo ricordare che l’altezza cade perpendicolarmente sul punto medio della base, così da dividere il triangolo isoscele in 2 triangoli rettangoli.
Sfruttando il teorema di Pitagora su questo triangolo venutosi a formare, otteniamo:
![]() .
.
Sostituendo nell’ultima le due equazioni precedenti, otteniamo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Visto che ![]() è negativa, questa soluzione non è accettabile in quanto una misura deve essere necessariamente positiva.
è negativa, questa soluzione non è accettabile in quanto una misura deve essere necessariamente positiva.
Quindi l’unica soluzione accettabile è: ![]() , da cui
, da cui
![]()
![]()
![]()
![]()
Altri esercizi simili:
- Esercizi equazioni di secondo grado: Problema 1 di geometria piana
- Esercizi equazioni di secondo grado: Problema 2 di geometria piana
- Esercizi equazioni di secondo grado: Problema 3 di geometria piana
- Esercizi equazioni di secondo grado: Problema 4 di geometria piana
- Esercizi equazioni di secondo grado: Problema 5 di geometria piana
- Esercizi equazioni di secondo grado: Problema 6 di geometria piana
- Esercizi equazioni di secondo grado: Problema 7 di geometria piana
- Esercizi equazioni di secondo grado: Problema 8 di geometria piana
- Esercizi equazioni di secondo grado: Problema 9 di geometria piana
- Esercizi equazioni di secondo grado: Problema 10 di geometria piana
- Esercizi equazioni di secondo grado: Problema 11 di geometria piana
- Esercizi equazioni di secondo grado: Problema 12 di geometria piana
(Questa pagina è stata visualizzata da 1369 persone)