Soluzione e svolgimento del seguente problemi di geometria piana.
- In un rettangolo la base supera di 24 cm i
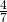 dell’altezza. Determinare il perimetro del rettangolo sapendo che l’area è di 448 cm
dell’altezza. Determinare il perimetro del rettangolo sapendo che l’area è di 448 cm
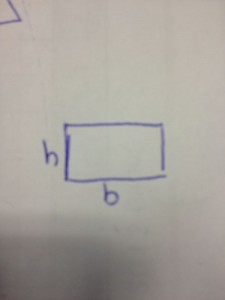
Definiamo con ![]() la base, con
la base, con ![]() l’altezza del rettangolo. In base ai dati otteniamo:
l’altezza del rettangolo. In base ai dati otteniamo:
![]()
![]()
Per i calcoli omettiamo le unità di misure, quindi, sostituendo il valore di ![]() nella seconda otteniamo:
nella seconda otteniamo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ovviamente ![]() sarà non accettabile perchè negativa, quindi l’unica soluzione accettabile sarà:
sarà non accettabile perchè negativa, quindi l’unica soluzione accettabile sarà: ![]() .
.
Quindi la base sarà:
![]()
e il perimetro sarà:
![]() .
.
Altri esercizi simili:
- Esercizi equazioni di secondo grado: Problema 1 di geometria piana
- Esercizi equazioni di secondo grado: Problema 2 di geometria piana
- Esercizi equazioni di secondo grado: Problema 3 di geometria piana
- Esercizi equazioni di secondo grado: Problema 4 di geometria piana
- Esercizi equazioni di secondo grado: Problema 5 di geometria piana
- Esercizi equazioni di secondo grado: Problema 6 di geometria piana
- Esercizi equazioni di secondo grado: Problema 7 di geometria piana
- Esercizi equazioni di secondo grado: Problema 8 di geometria piana
- Esercizi equazioni di secondo grado: Problema 9 di geometria piana
- Esercizi equazioni di secondo grado: Problema 10 di geometria piana
- Esercizi equazioni di secondo grado: Problema 11 di geometria piana
- Esercizi equazioni di secondo grado: Problema 12 di geometria piana
(Questa pagina è stata visualizzata da 747 persone)