Soluzione e svolgimento del seguente problemi di geometria piana.
- Trovare l’altezza di un triangolo di base 12 cm tale che la sua area sia equivalente a quella di un quadrato il cui lato è
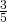 dell’altezza del triangolo.
dell’altezza del triangolo.
Qui bisogna ragionare un attimo sui dati…
Vediamo di spiegare bene cosa abbiamo:
Chiamiamo con ![]() e
e ![]() l’altezza e la base del triangolo, e con
l’altezza e la base del triangolo, e con ![]() il lato del quadrato. Avremo che:
il lato del quadrato. Avremo che:
![]()
![]()
![]() .
.
Il nostro problema sarà tutto nella seconda equazione, in quanto avremo, sostituendo:
![]()
![]()
![]()
Dividendo tutto per ![]() , e supponendo che questa sia diversa da
, e supponendo che questa sia diversa da ![]() (un lato non può avere misura nulla…), otteniamo:
(un lato non può avere misura nulla…), otteniamo:
![]()
![]()
Altri esercizi simili:
- Esercizi equazioni di secondo grado: Problema 1 di geometria piana
- Esercizi equazioni di secondo grado: Problema 2 di geometria piana
- Esercizi equazioni di secondo grado: Problema 3 di geometria piana
- Esercizi equazioni di secondo grado: Problema 4 di geometria piana
- Esercizi equazioni di secondo grado: Problema 5 di geometria piana
- Esercizi equazioni di secondo grado: Problema 6 di geometria piana
- Esercizi equazioni di secondo grado: Problema 7 di geometria piana
- Esercizi equazioni di secondo grado: Problema 8 di geometria piana
- Esercizi equazioni di secondo grado: Problema 9 di geometria piana
- Esercizi equazioni di secondo grado: Problema 10 di geometria piana
- Esercizi equazioni di secondo grado: Problema 11 di geometria piana
- Esercizi equazioni di secondo grado: Problema 12 di geometria piana
(Questa pagina è stata visualizzata da 675 persone)