Esercizi equazioni di secondo grado: Problema 2 di geometria piana

0

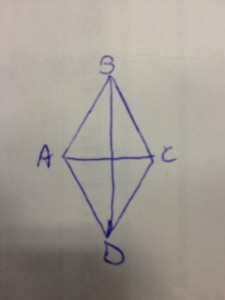
Soluzione e svolgimento del seguente problemi di geometria piana.

 

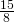  • L’area di un rombo è 960 cm^2, una diagonale è \frac {15}{8} dell’altra, trovare il perimetro del rombo.

Chiamiamo con \overline {BD}=x e \overline {AC}=y le 2 diagonali del rombo.

Dai dati sappiamo che:

A=960 \mbox { cm}^2
\frac x y = \frac {15}{8}

Dalla prima otteniamo:

\frac 1 2 x*y= 960 \mbox { cm}^2

Dalla seconda otteniamo :
x=\frac {15}{8}y

Sostituendo il valore della x appena trovato, nella prima otteniamo l’equazione:

\frac 1 2 \frac {15}{8} y*y= 960 \mbox { cm}^2
\frac {15}{16} y^2= 960 \mbox { cm}^2
y^2=\frac {16}{15}960 \mbox { cm}^2
y^2=1024 \mbox { cm}^2
y=\sqrt {1024 }\mbox { cm}= 32 \mbox { cm}

Escludiamo a priori la soluzione negativa, in quanto un lato non potrà mai avere misura negativa…

Da qui, sostituendo il valore della y nella seconda equazione otteniamo:

x=\frac {15}{8} y=\frac {15}{8} 32 \mbox { cm} =60 \mbox { cm}

Per trovare il perimetro, dobbiamo ricordare che tra le proprietà del rombo c’è quella di avere tutti e 4 i lati uguali, e che le diagonali si intersecano nel loro punto medio perpendicolarmente; quindi, per trovare il lato del rombo, basta semplicemente applicare il teorema di pitagora sul triangolo rettangolo formato dalle due semidiagonali, (i 2 cateti) e dal lato del rombo che funge da ipotenusa.

Chiamando con \overline{AB}=l il lato del rombo otteniamo così:

l=\sqrt {(\frac {x}{2})^2+(\frac {y}{2})^2}=\sqrt {(\frac {60}{2})^2+(\frac {32}{2})^2}\mbox { cm}=\sqrt {(30)^2+(16)^2}\mbox { cm}=\sqrt {900 +256 }\mbox { cm}=\sqrt {1156 }\mbox { cm}=34 \mbox { cm}

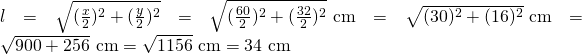
Quindi il perimetro sarà:

2p=4l=4*34 \mbox { cm}= 136 \mbox { cm}

Altri esercizi simili:

(Questa pagina è stata visualizzata da 905 persone)

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *