QUESTIONARIO
- Un triangolo ha area 3 e due lati che misurano 2 e 3. Qual è la misura del terzo lato? Si giustifichi la risposta.
- Se la funzione
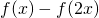 ha derivata 5 in
ha derivata 5 in 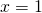 e derivata 7 in
e derivata 7 in 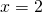 , qual è la derivata della funzione
, qual è la derivata della funzione 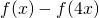 in
in 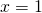 ?
? - Si considerino, nel piano cartesiano, i punti A (2; -1) e B (- 6; – 8). Si determini l’equazione della retta passante per B e avente distanza massima da A.
- Di un tronco di piramide retta a base quadrata si conoscono l’altezza h e i lati a e b delle due basi. Si esprima il volume V del tronco in funzione di a, b e h, illustrando il ragionamento seguito.
- In un libro si legge: “se per la dilatazione corrispondente a un certo aumento della temperatura un corpo si allunga (in tutte le direzioni) di una certa percentuale (p.es. 0,38%), esso si accresce in volume in proporzione tripla (cioè dell’1,14%), mentre la sua superficie si accresce in proporzione doppia (cioè di 0,76%)”. È così? Si motivi esaurientemente la risposta.
- In un gruppo di 10 persone il 60% ha occhi azzurri. Dal gruppo si selezionano a caso due
persone. Quale è la probabilità che nessuna di esse abbia occhi azzurri?
- Si mostri, senza utilizzare il teorema di l’Hopital, che
![Rendered by QuickLaTeX.com \[ \lim_{x \to \pi } \frac {e^{senx}-e^{sen(\pi)}}{x-\pi}=-1\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-7e60519a2c59077e0568dd3c3a04bf8a_l3.png)
- Tre amici discutono animatamente di numeri reali. Anna afferma che sia i numeri razionali che
- Si stabilisca per quali valori
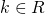 l’equazione
l’equazione 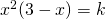 ammette due soluzioni distinte
ammette due soluzioni distinte
Altri esercizi simili
- Problema 1 P.N.I. 2013
- Problema 1 Scientifico 2013
- Problema 2 P.N.I. 2013
- Problema 2 Scientifico 2013
- Quesiti P.N.I. 2013
- Quesiti Scientifico 2013
(Questa pagina è stata visualizzata da 41 persone)